Capítulo 6 O POÇO RETANGULAR INFINITO

6.1 Introdução

Nas [ seções 4.5 e 4.6 ], apresentamos o operador associado ao momento linear [ ˆp$\hat{p}$ ] e o operador associado à posição [ ˆx$\hat{x}$ ]. Agora vamos tratar de um operador que está em correspondência com a energia total de uma onda de matéria, o operador da energia total ˆH$\hat{H}$.

O operador ˆH$\hat{H}$ é composto de dois termos. Em relação à função alvo, o primeiro termo instrui que realizemos a derivada segunda dessa função e, depois, multipliquemos o resultado dessa derivada por uma constante. O segundo termo instrui que a função alvo seja multiplicada pelo potencial que perturba o espaço em que a partícula se encontra. Matematicamente, o operador ˆH$\hat{H}$ é assim:

ˆH=−ℏ22md2dx2+V(x).

A equação de autovalor do operador da energia total é do tipo:

ˆHψE(x)=EψE(x).

Onde o subscrito E subentende que a autofunção ψE está associada ao autovalor E.

Substituindo (6.1) em (6.2), temos:

−ℏ22md2ψE(x)dx2+V(x)ψE(x)=EψE(x).

Lembramos que (6.3) é a equação de Schrödinger independente do tempo [ seção 1.3 ].

O caso introdutório, no manuseio do operador da energia total, será o da partícula livre.

Nota: o livre de parícula livre é para indicar que tal partícula não sofre restrições de movimento, é para indicar que V(x)=0.

Na ausência de potencial, a equação (6.3) fica mais simples de resolver:

−ℏ22md2ψE(x)dx2=EψE(x).

Podemos chamar,

k2=2mEℏ2.

Desse modo, a equação (6.4) fica compacta,

d2ψE(x)dx2=−k2ψE(x),

e de solução trivial,

ψE(x)=Ceikx.

Na [ seção 4.5 ], vimos (6.7) como solução do operador ˆp. Agora vemos (6.7) como solução do operador ˆH. Concluímos, então, que na falta de um potencial, os autoestados de ˆp também são autoestados de ˆH.

Agora sobre a energia, podemos isolar E da equação (6.5):

E(k)=ℏ2k22m.

Visto que o número de onda k pode percorrer de −∞ até +∞, a energia da partícula livre é contínua, 0<E<+∞.

6.2 A função de onda da posição

Na introdução [ seção 6.1 ], resolvemos o caso da partícula livre. Agora vamos tratar do caso da partícula confinada em um segmento do espaço. O poço de potencial que causa o confinamento terá paredes de altura infinita, seu perfil é apresentado na Fig. 6.1.

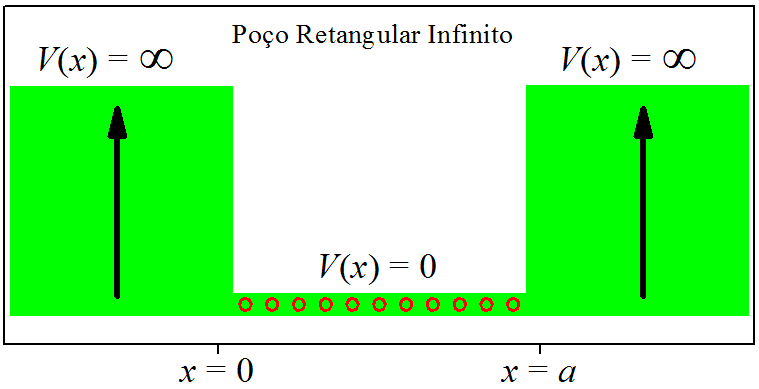
Figura 6.1: O poço retangular infinito.

Matematicamente, o poço retangular infinito pode ser escrico assim:

V(x)=0,se  0<x<a,=∞,se  x⩽0  e  x⩾a.

Basicamente, ficamos com duas equações de Schrödinger para resolver: uma dentro do poço [ com V=0 ] e outra fora [ com V=∞ ].

Dentro do poço, temos a solução da partícula livre, mas precisamos pensar em duas ondas se sobrepondo [ seção 1.4 ]: uma onda caminhando para a direita, com função Aeikx, e outra onda caminhando no sentido contrário, com função Be−ikx. O motivo de escolhermos essas duas ondas é para levar em conta as reflexões que ocorrem nas paredes do poço. Assim, as ondas que caminham em sentidos opostos sofrem interferência uma da outra. Como se vê, o estado dentro do poço é um estado de superposição:

ψ(x)=Aeikx+Be−ikx.

Agora vamos analisar o que acontece fora do poço.

A partícula não pode ser encontrada fora do poço, pois o potencial é infinito. Não poder ser encontrada significa ψ=0. Então ψ=0 deve ocorrer nas duas interfaces: ψ(0)=0 e ψ(a)=0.

Substituindo ψ(0)=0 na equação (6.10), encontramos:

0=A+B⟹B=−A.

O resultado (6.11), levado à equação (6.10), simplifica a solução dentro do poço:

ψ(x)=A(eikx−e−ikx).

Usando a relação matemática e±ikx=cos(kx)±sen(kx) na equação (6.12), ficamos com:

ψ(x)=2iAsen(kx).

A solução (6.13) deve passar pelo processo de normalização:

∫+∞−∞|ψ(x)|2dx=1⟹4|A|2∫a0|sen(kx)|2dx=1.

Em tabelas de integral encontramos:

∫a0|sen(kx)|2dx=a2.

Ao substituir o resultado (6.15) em (6.14):

|A|2=A∗A=12a.

O resultado (6.16) não esclarece se A é um número real ou complexo. Isso fica para nós escolhermos. É preferível que a solução dentro do poço seja uma função real, para que isso ocorra, podemos escolhemos que A seja o seguinte número complexo:

A=1i√2a.

Substituindo (6.17) em (6.13), a função de onda dentro do poço passa a ser:

ψ(x)=√2asen(kx).

Ainda falta analisar a condição ψ(a)=0. Então, vamos substituir essa condição na equação (6.18):

0=√2asen(ka).

O que torna a equação (6.19) verdadeira é:

ka=nπ⟹kn=nπa,   com  n=1,2,3...

Descartamos em (6.20) a possibilidade n=0 por se tratar de uma onda inexistente. Ademais, incorporamos o subscrito n na notação. Ele é chamado de número quântico principal e indica que a grandeza é discreta: acabamos de “descobrir” a quantização!

Nota: A seção 6.6 vai aprofundar o entendimento do papel do número de onda kn no poço retangular infinito.

Levando o resultado (6.20) em (6.18), chegamos à solução final do poço retangular infinito:

ψn(x)=√2asen(nπax).

Por causa da quantização do número de onda (6.20), os estados (6.21) dentro do poço são discretos.

Sobre a energia, enquanto a partícula livre possui um espectro de energia contínuo [ seção 6.1 ], também por causa de (6.20), a partícula confinada no poço retangular infinito apresenta um espectro discreto, ou seja, a energia é quantizada:

En=ℏ2k2n2m.

∙  Um exemplo numérico.

Nosso objetivo é ver o contorno das funções de onda e determinar as energias de confinamento. Dentro de um poço infinito de largura a=100 Å, vamos colocar um eletron. Sabemos que a massa do elétron é m=9,1×10−31kg. Também sabemos que ℏ=1,055×10−34Js, que é o mesmo que ℏ=6,582×10−16eVs. Colocando esses valores nas relações (6.22) e (6.20), calculamos para n= 1, 2, 3 e 4:

E1=3,8 meV,k1=3,14×108 m−1,E2=15,0 meV,k2=6,28×108 m−1,E3=33,9 meV,k3=9,43×108 m−1,E4=60,2 meV,k4=12,57×108 m−1.

A Fig. 6.2 compara as energias do elétron confinado no poço retangular infinito com as energias do elétron livre. Enquanto a partícula livre possui um espectro contínuo, torna-se claro o fenômeno da quantização da energia manifestado pela partícula confinada.

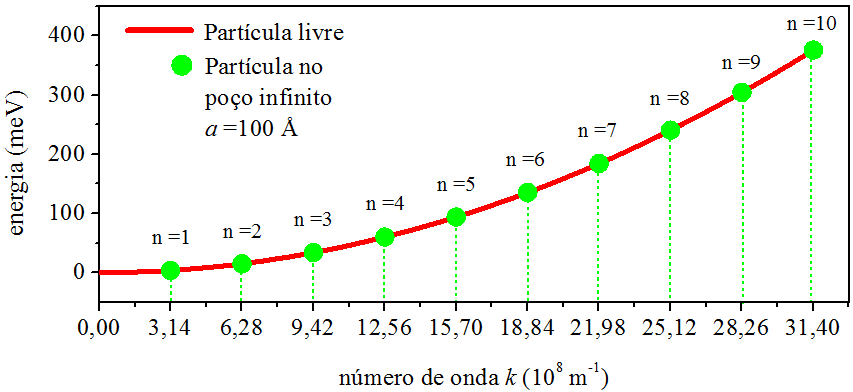
Figura 6.2: A quantização da energia.

Submetendo os mesmos dados em (6.21), a Fig. 6.3 apresenta o perfil das funções de onda da posição.

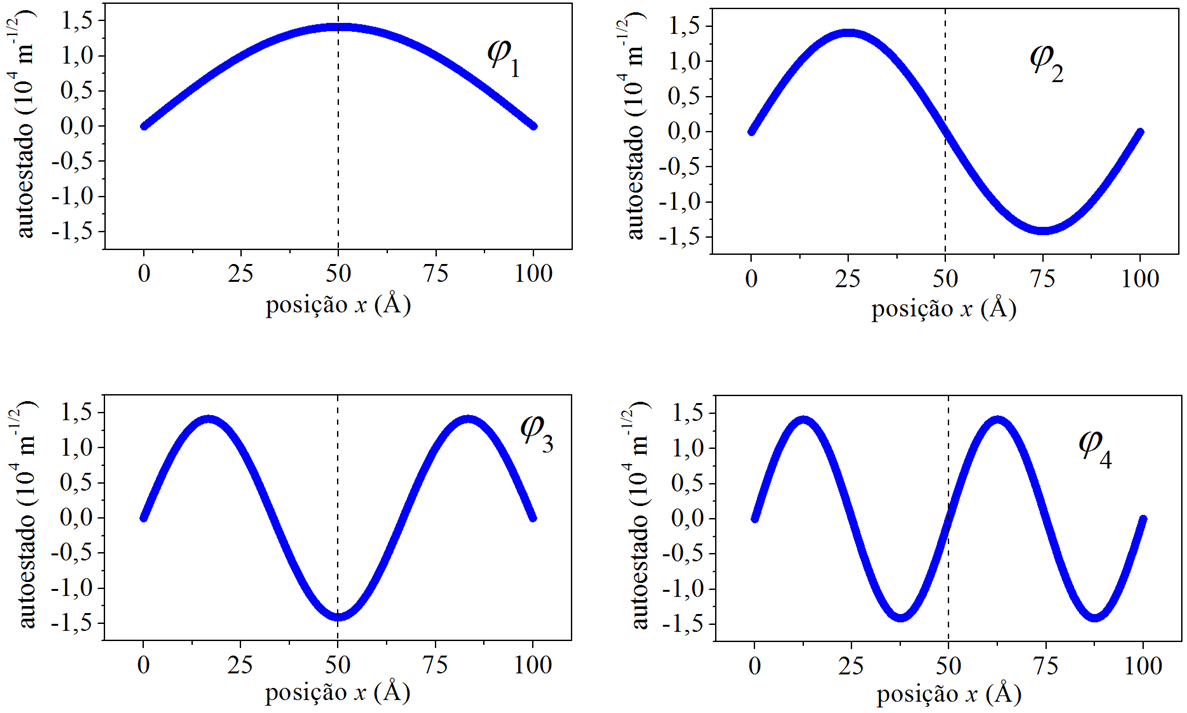
Figura 6.3: As funções de onda da posição.

As funções de onda são pares ou ímpares com respeito ao centro do poço, à medida que o número quântico principal n aumenta. Também, com o aumento de n, cresce o número de zeros da solução. Uma inspeção visual nos permite dizer que o número de zero é igual a n−1.

6.3 A densidade de probabilidade da posição

Tendo determinado as funções de onda da posição para o poço retangular infinito [ Fig. 6.3 ], a densidade de probabilidade da posição se escreve,

|ψn(x)|2=2asen2(nπax),

e tem o perfil apresentado na Fig. 6.4 [repetindo os mesmos dados da Fig. 6.3].

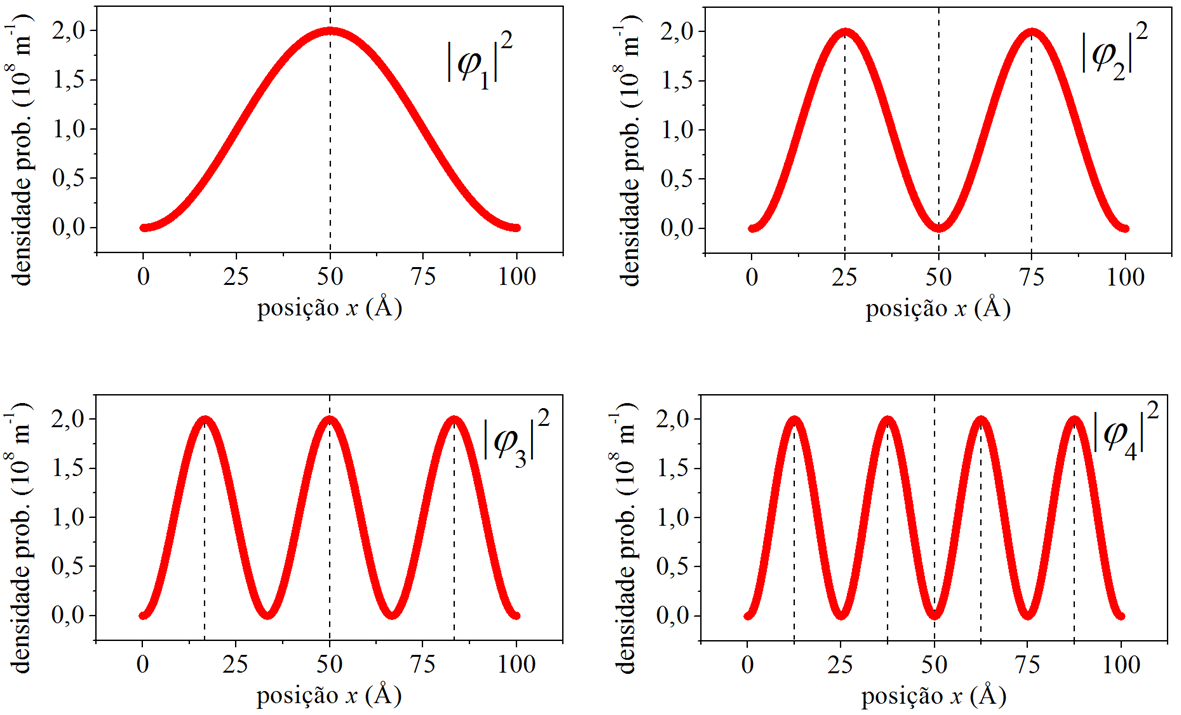
Figura 6.4: As densidades de probabilidade da posição.

A densidade de probabilidade da posição oscila [ seção 3.5 ]. A quantidade de máximos da oscilação é igual n, e o período espacial da oscilação é igual a δx=a/n. Por exemplo, a densidade de probabilidade n=1 apresenta apenas 1 máximo e δx=100 Å [ devemos lembrar que o poço em questão possui largura a=100 Å ]. Ela não é periódica. As demais densidades de probabilidade são periódicas. Por exemplo, densidade de probabilidade n=2 possui 2 máximos e δx=50 Å, e assim por diante. Para n elevado, o período espacial se torna tão pequeno que a densidade de probabilidade tende a se comportar como uma constante, na qual as posições são igualmente prováveis. Dizemos, então, que a partícula deixa de ter caráter quântico e passa a agir como uma partícula clássica. A Fig. 6.5 ilustra a perda do caráter quântico, mostrando a densidade de probabilidade n=100, com 100 picos e δx=1 Å.

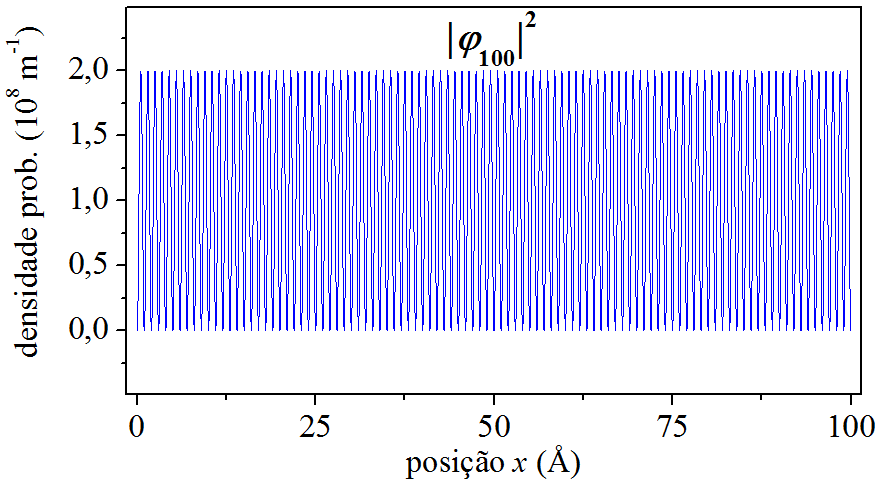
Figura 6.5: A perda do caráter quântico para n=100.

6.4 O desvio padrão da posição

As médias ponderadas com a densidade de probabilidade da posição são calculadas por integrais que cobrem todo espaço [ seção 3.4 ]. Mas, por causa das funções de onda do poço infinito só existirem dentro do poço, as integrações se limitam à largura do poço:

⟨x⟩n=∫a0x|ψn(x)|2 dx=a2,

⟨x2⟩n=∫a0x2|ψn(x)|2 dx=a23(1−32π2n2).

Com os resultados acima, poderemos determinar o desvio padrão da posição:

Δxn=√⟨x2⟩n−⟨x⟩2n=a√112−12π2n2.

Se montarmos uma experiência para medir a posição de uma partícula preparada no autoestado ψn de um poço infinito de largura a, firmada na seguinte hipótese: após cada medição, a partícula é colocada novamente em ψn, temos motivos estatísticos para afirmar que a posição média dessa partícula será a/2 – pouco importando o estado da partícula, pois a média (6.25) independe de n.

Sobre o desvio padrão (6.27), percebemos que ele aumenta à medida que a partícula é colocada em autoestados superiores. No limite de n tendendo ao infinito, o desvio padrão tende ao valor limite igual a a/√12. Considerando o poço retangular infinito de largura a=100 Å, a Fig. 6.6 mostra o comportamento de Δxn em função de n.

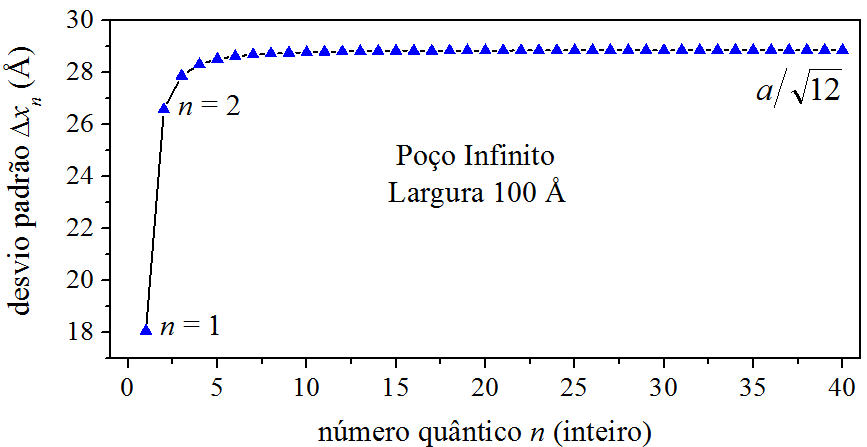
Figura 6.6: Desvio padrão em função do número quântico principal.

Como vemos na Fig. 6.6, o desvio padrão parte de Δx1=18,0 Å, aumenta para Δx2=26,6 Å e, ao redor de n=20, se acomoda no patamar 28,9 Å. Observa-se que a posição da partícula fica cada vez mais incerta. Isso é reflexo do perfil da densidade de probabilidade: Na Fig. 6.4, a densidade de probabilidade para n alto é mais dispersiva que a densidade de probabilidade para n baixo.

6.5 A função de onda do momento

Na [ seção 5.2 ], escrevemos a onda truncada como um pacote de autoestados do operador do momento ˆp [ seção 4.5 ]. Agora vamos repetir o procedimento com as funções de onda da posição provenientes do poço retangular infinito [ seção 6.2 ]:

ψn(x)=1√2π∫+∞−∞ϕn(k)eikxdk.

O coeficiente da superposição é interpretado como função de onda do momento. É determinado através da transformada de Fourier inversa:

ϕn(k)=1√2π∫+∞−∞e−ikxψn(x)dx=1√2π√2a∫+∞−∞e−ikxsen(nπax)dx.

A dica para resolver a integral (6.29) é fazer a seguinte substituição:

sen(nπax)=einπax−e−inπax2i.

Exige um pouco de trabalho até chegarmos à expressão final da função de onda do momento:

ϕn(k)=1i√a4πe−i(nπ2−ka2)××(sen(nπ2−ka2)nπ2−ka2+(−1)n+1sen(nπ2+ka2)nπ2+ka2).

Lembrando que kn=nπa, eis nossa “equaçãozinha” alternativa:

ϕn(k)=1i√a4πe−i[a2(kn−k)]××(sen[a2(kn−k)]a2(kn−k)+(−1)n+1sen[a2(kn+k)]a2(kn+k)).

6.6 A densidade de probabilidade do momento

Na [ seção 6.5 ], deduzimos a função de onda do momento. Agora podemos escrever a densidade de probabilidade do momento:

|ϕn(k)|2=a4π××(sen(nπ2−ka2)nπ2−ka2+(−1)n+1sen(nπ2+ka2)nπ2+ka2)2.

Ou, na forma que exprime kn:

|ϕn(k)|2=a4π××(sen[a2(kn−k)]a2(kn−k)+(−1)n+1sen[a2(kn+k)]a2(kn+k))2.

Alimentando (6.33) ou (6.34) com os mesmos dados da [ seção 6.2 ], podemos graficar a densidade de probabilidade do momento e discutir seu comportamento. Por exemplo, para o elétron no estado ψ1 do poço retangular infinito de largura a=100 Å, a curva de |ϕ1|2 é vista na Fig. 6.7

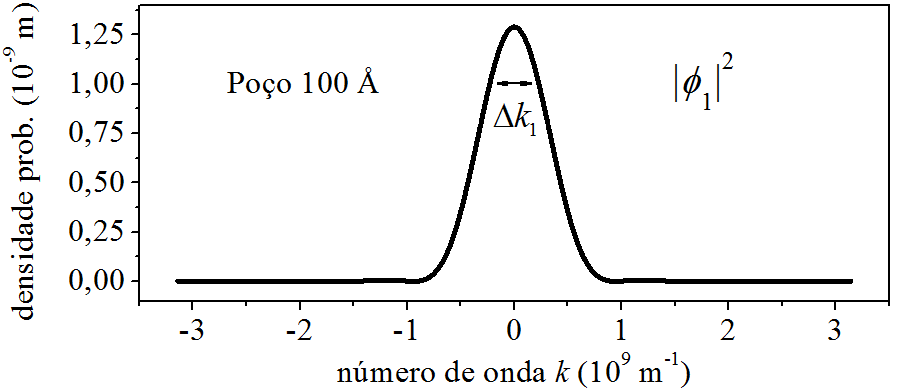
Figura 6.7: Densidade de probabilidade do momento para n=1.

Observamos que há apenas um pico, em torno de k=0. Observamos também que há uma gama de momentos distribuídos ao longo do eixo k. Isso nos faz pensar que o elétron ocupando o estado ψ1 do poço infinito, não está em um estado de momento único, mas numa superposição de estados de momentos variados. Em uma medição do momento do elétron, os valores ao redor do pico são os mais prováveis de ocorrer, já os afastados, também poderão ocorrer, mas tendem a não acontecer. Tratando de um segmento de momentos, a área que começa em k=g1 e termina em k=g2, fornece a probabilidade de um resultado estar entre g1 e g2:

Pr(g1<k<g2)=∫g2g1|ϕ1(k)|2dk.

O k1, de valor π/a=3,14×108 m−1, é o número de onda − geométrico − que desenha a função de onda da posição ψ1 pelo espaço da posição. Ele entra na expressão da função de onda do momento ϕ1, contribuindo para o desenho do pico de eventos mais prováveis e da deriva de eventos menos próváveis. O k1 não é o momento exclusivo do elétron. Seria errado multiplicar o seu valor por ℏ e dizer “o momento exclusivo do elétron é ℏk1.” O momento ℏk do elétron tem natureza probabilística, e não geométrica, por exemplo, tem probabilidade (6.35) de ocorrer entre os valores g1 e g2.

E se o elétron subir de estado, indo para ψ2? A Fig. 6.8 mostra a curva de |ϕ2|2.

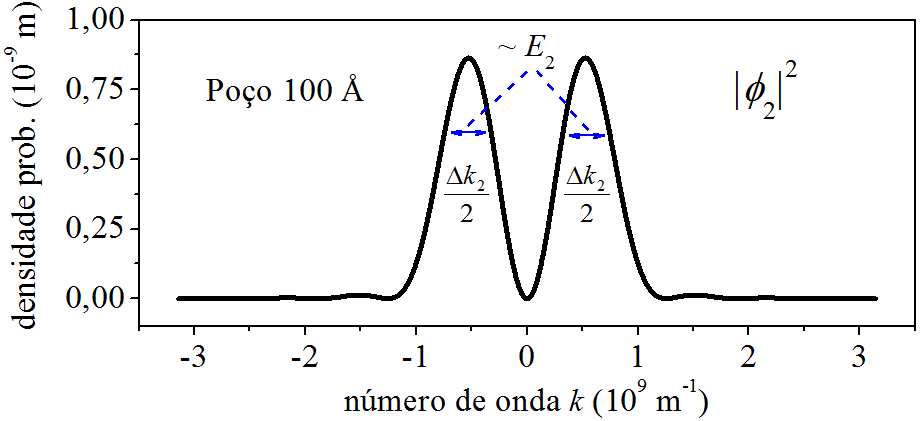
Figura 6.8: Densidade de probabilidade do momento para n=2.

Agora a densidade de probabilidada do momento apresenta dois picos. Em uma medição do momento do elétron, os valores ao redor dos picos 1 e 2 são os mais prováveis de ocorrer. Notem que eles se afastaram de k=0. É útil comparar as Figs. 6.7 e 6.8. Para facilitar a visão, juntamos as duas na Fig. 6.9.

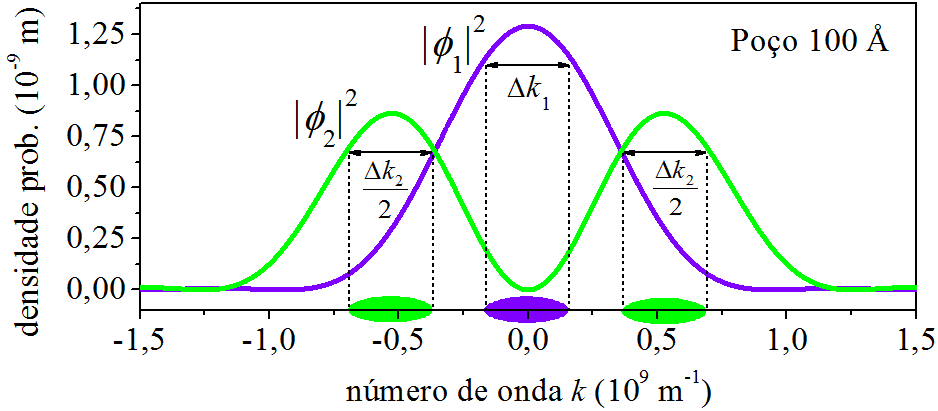
Figura 6.9: Densidades de probabilidade do momento para n=1 e n=2.

O elétron em ψ1 concentra os momentos ao redor de k=0, manifesta valores baixos. Já em ψ2, manifesta valores mais altos, ao redor de k=±5×108 m−1. Isso é decorrente da energia do elétron nos dois casos. Enquanto que em n=1, ele está com E1=3,8 meV, em n=2, sua energia é mais alta, E2=15,0 meV. Usando da linguagem coloquial: “Um elétron energético possui momento alto.” E quanto maior a energia do elétron, maior será os valores de momento que ele pode manifestar. Isso é claro observando as curvas de |ϕ3|2 e |ϕ4|2, Fig. 6.10. Nos dois casos, os picos estão acima de k=±5×108 m−1.

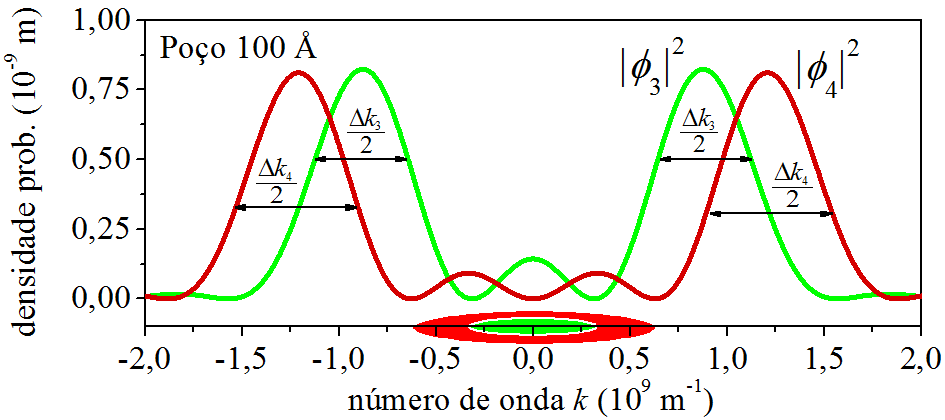
Figura 6.10: Densidades de probabilidade do momento para n=3 e n=4.

A novidade que aparece na Fig. 6.10, são os momentos menos prováveis entre os valores k=±5×108 m−1.

Mais sobre o papel do número de onda.

O kn “posiciona” o pico da curva de |ϕn|2. O pico não sai exatamente no mesmo valor do kn, mas fica próximo, conforme se vê na Fig. 6.11, casos n=1 até n=4. É consequência da mistura! A equação (6.34) é formada por dois termos. Cada termo individual tem pico em kn, por causa dos denominadores (kn−k) e (kn+k). Vemos a cointribuição do primeiro termo de (6.34) através da Fig. 6.12. Veja agora como os picos se posicionam exatamente nos valores de kn.

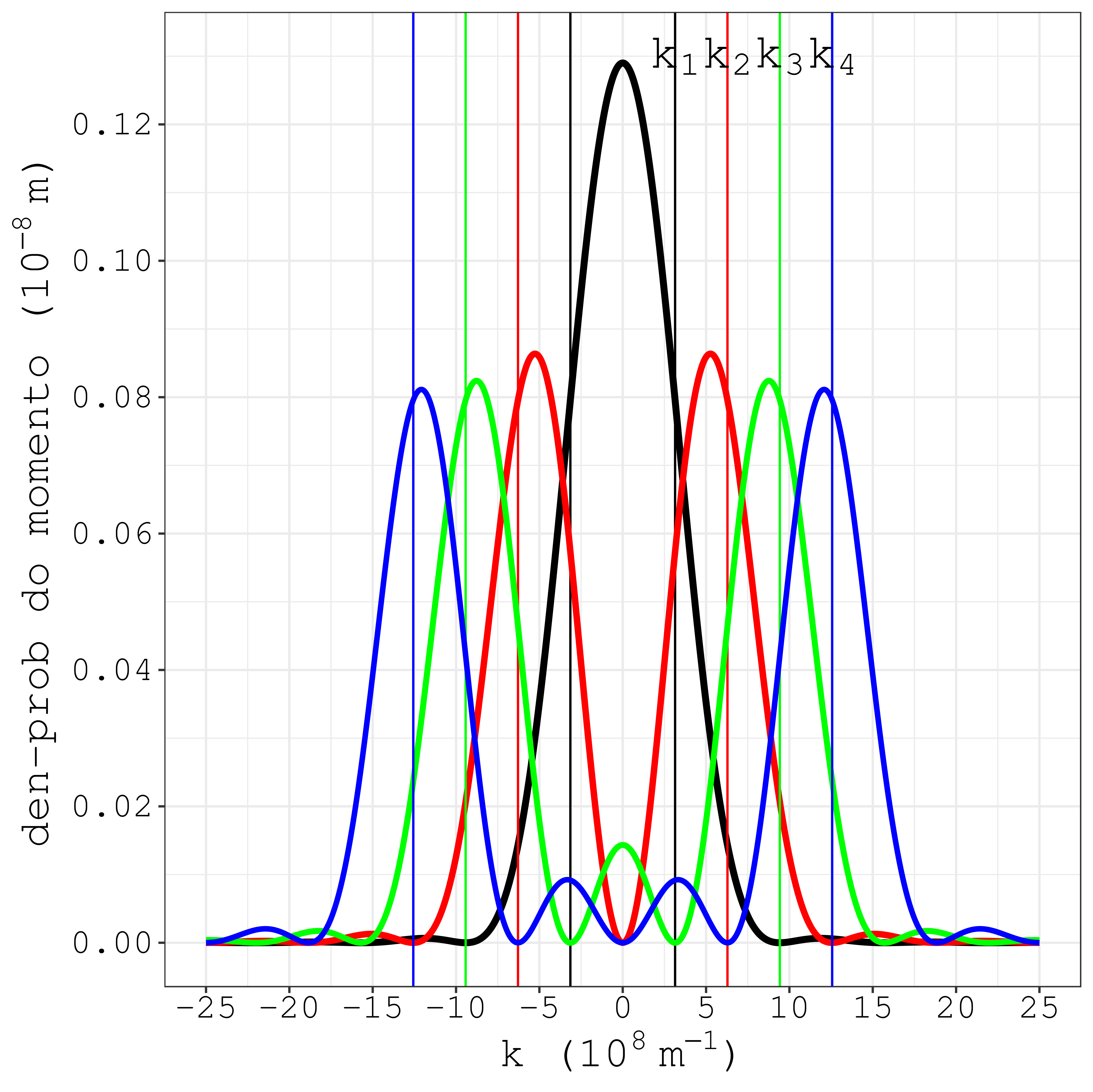
Figura 6.11: A localização do kn, em relação aos picos de |ϕn|2, para os casos n=1 até n=4.

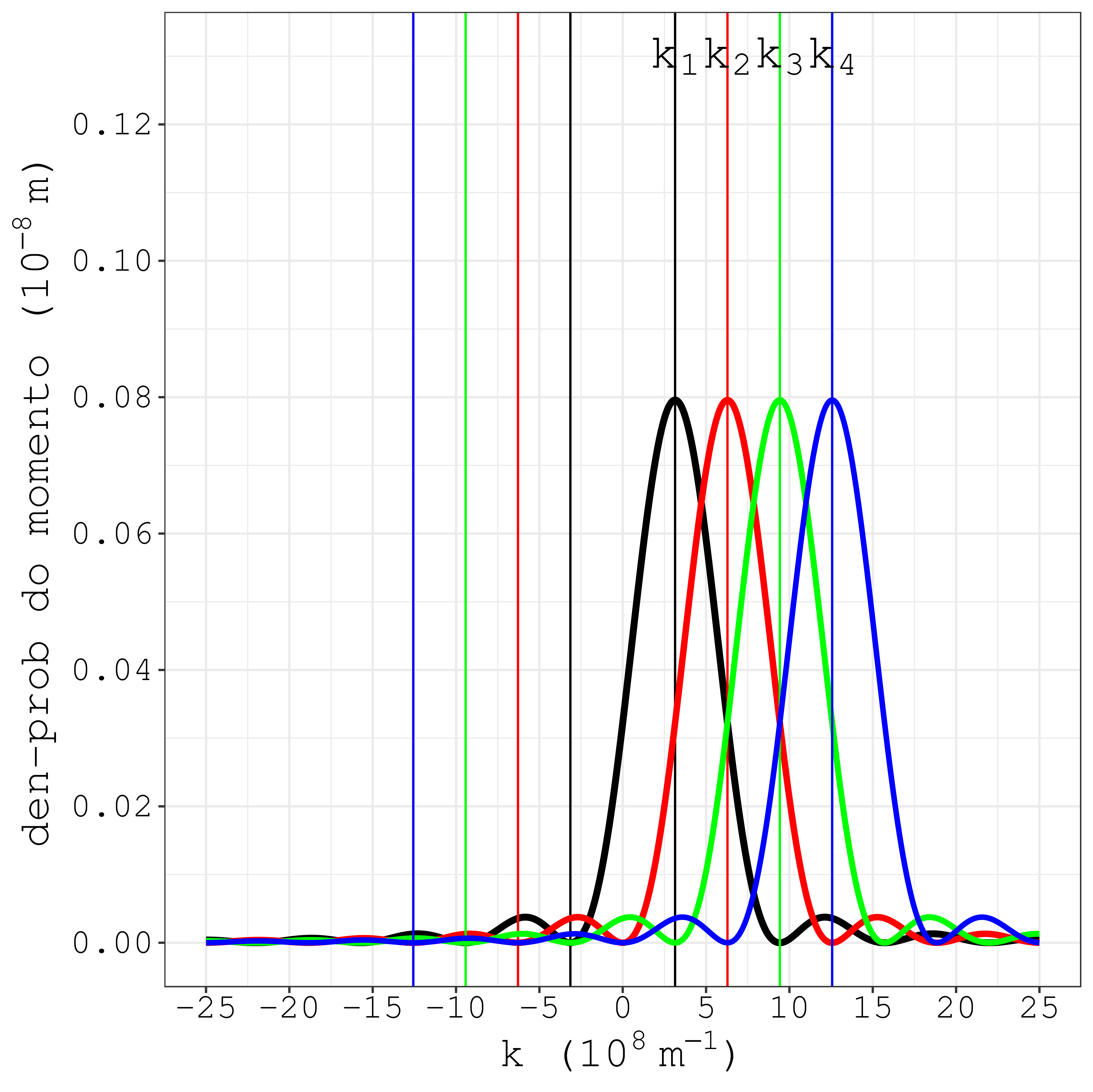
Figura 6.12: Apenas a contrubuição do primeiro termo da equação (6.34).

6.7 O desvio padrão do momento

Na [ seção 3.4 ], vimos como determinar o resultado médio de uma experiência montada para medir a posição de uma partícula. Aqui vamos escrever a mesma equação, mas numa forma que ressalte o operador quântico:

⟨x⟩=∫+∞−∞ψ∗(x)ˆxψ(x)dx.

A formulação (6.36) também se aplica a outros casos. Por isso, resultado médio e o resultado médio, ao quadrado, do momento, assim se equacionam:

⟨k⟩=∫+∞−∞ψ∗(x)ˆkψ(x)dx,

⟨k2⟩=∫+∞−∞ψ∗(x)ˆk2ψ(x)dx.

Lembrando que [ seção 4.2 ]:

ˆk=−iddx.

Escrevemos ˆk2=ˆkˆk:

ˆk=−d2dx2.

Substituindo as funções de onda da posição referentes ao poço retangular infinito [ seção 6.2 ] nas equações (6.37) e (6.38), e resolvendo as integrais resultantes, encontramos:

⟨k⟩n=0,

⟨k2⟩n=(nπa)2.

Com os resultados acima, determinamos o desvio padrão do momento:

Δkn=√⟨k2⟩n−⟨k⟩2n=nπa.

Como podemos interpretar esses resultados?

Interpretação 1: Se montarmos uma experiência para medir o momento de uma partícula preparada em um estado de um poço retangular infinito, firmada na seguinte hipótese: após cada medição, a partícula é colocada novamente no mesmo estado, segundo (6.41), há motivos estatísticos para afirmar que o momento médio dessa partícula será zero.

Interpretação 2: Se uma partícula, preparada em um estado de um poço retangular infinito, subir de estado, a medição de seu momento ficará mais incerta, pois o desvio padrão do momento (6.43) é diretamente proporcional ao número quantico principal n.

6.8 O princípio da incerteza

Tendo em mãos as expressões das incertezas da posição [ seção 6.4 ] e do momento [ seção 6.7 ], podemos ver como fica o produto delas:

ΔxnΔkn=√n2π212−12.

Por causa de Δxn ser diretamente proporcional à largura do poço [ a ], e Δkn ser inversamente proporcional à largura a, produto (6.44) não depende da largura do poço. Ademais, esse produto aumenta com o aumento do número quântico n.

O menor valor possível para o produto (6.44) acontece para o estado n=1:

Δx1Δk1=0,57.

Na [ seção 2.1 ], introduzimos o princípio da incerteza de Heisenberg. Aqui vamos escrever a mesma relação, porém sem a constante ℏ:

ΔxΔk⩾0,50.

Comparando (6.45) e (6.46), concluímos que o poço retangular infinito confirma a relação de Heisenberg.

6.9 O princípio da incerteza, informal

As funções de onda da posição, ψn, do poço retangular infinito, formam um base discreta [ seção 6.2 ]. Um novo estado pode ser construído por meio dessa base, através de uma combinação linear. Em certo tempo t, esse novo estado pode ser assim escrito:

Ψ(x,t)=∞∑n=1cnψn(x)e−iEnℏt.

∙  Vamos trabalhar (6.47) com t=0 para simplificar a notação:

Ψ(x,t)=∞∑n=1cnψn(x).

E para simplificar ainda mais, vamos limitar a discussão para o caso da superposição ser composta de apenas dois autoestados:

Ψ(x,t)=c1ψ1+c2ψ2.

Em uma experiência montada para fazer a medição da energia de uma partícula preparada na superposição (6.49), o resultado médio da energia pode ser determinado por:

⟨E⟩=∫+∞−∞Ψ∗ˆHΨdx.

Substituindo (6.49) em (6.50):

⟨E⟩=∫+∞−∞(c∗1ψ∗1+c∗2ψ∗2)ˆH(c1ψ1+c2ψ2)dx.

Aqui está a equação de autovalor do operador da energia total:

ˆHψn=Enψn.

Aplicando (6.52) no lado direito de (6.51), ficamos com:

⟨E⟩=∫+∞−∞(c∗1ψ∗1+c∗2ψ∗2)(c1E1ψ1+c2E2ψ2)dx.

Fazendo as multiplicações dos termos entre os parênteses, e lembrando que as funções de onda da posição do poço retangular infinito são ortogonais, o resultado final é:

⟨E⟩=|c1|2E1+|c2|2E2.

Temos em (6.54), uma equação de média poderada pelos coeficientes |c1|2 e |c2|2. O valor de |c1|2, é a probabilidade de se registrar a energia E1. Analogamente, o valor de |c2|2, é a probabilidade de se registrar a energia E2. E, decorrente da normalização dos eventos:

|c1|2+|c2|2=1.

Repetindo o procedimento que levou à equação (6.54), determinamos o resultado médio, ao quadrado, da energia:

⟨E2⟩=|c1|2E21+|c2|2E22.

Com os resultados acima, encontramos o desvio padrão da energia:

ΔE=√⟨E2⟩−⟨E⟩2=√|c1|2|c2|2(E2−E1)2.

No caso dos coeficientes serem reais, temos:

ΔE=c1c2(E2−E1).

O resultado (6.58) mostra que a incerteza na energia é proporcional à energia que separa os estados n=1 e n=2.

∙  Chegou a hora de colocar números nas equações.

Considere um elétron confinado em um poço retangular infinito de largura a=100 Å. Obs.: Na [ seção 6.2 ], estão impressos os valores de E1 e E2. Considere também o elétron está na superposição (6.49) com c1=c2=√0,50:

Ψ(x,t)=√0,50ψ1+√0,50ψ2.

Utilizando (6.54) e (6.58), calculamos:

⟨E⟩=9,4 meV,ΔE=5,6 meV.

A superposição (6.59) gera uma distribuição de probabilidade discreta, com apenas dois resultados possíveis, E1 e E2, os quais possuem a mesma probabilidade de ocorrer, c21=c22=0,50. Ademais, a média (6.60) não coincide com os possíveis resultados da medição. Tudo pode ser visualizado no histograma da Fig. 6.13.

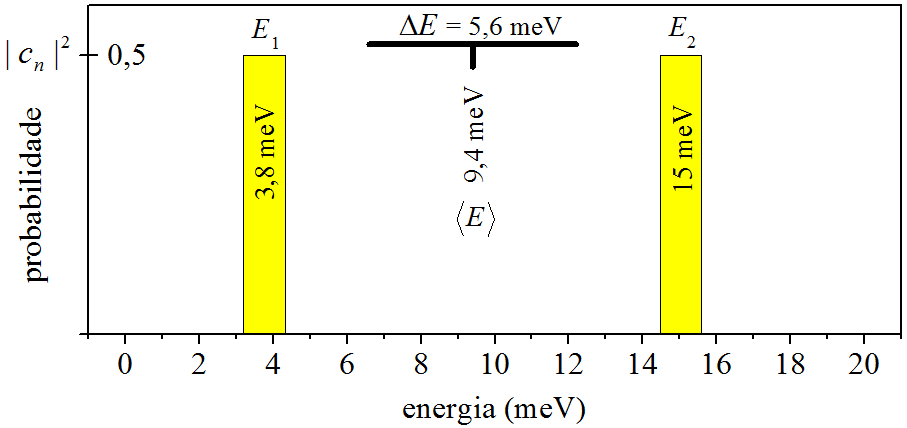
Figura 6.13: Distribuição de probabilidade gerada pela superposição (6.59).

∙  Agora voltaremos com o tempo.

O equivalente da situação (6.49) em t, é:

Ψ(x,t)=c1ψ1e−iE1ℏt+c2ψ2e−iE2ℏt.

O estado (6.62) gera a densidade de probabilidade [ ψn é real ]:

|Ψ(x,t)|2=(c∗1ψ1e+iE1ℏt+c∗2ψ2e+iE2ℏt)××(c1ψ1e−iE1ℏt+c2ψ2e−iE2ℏt)=|c1|2ψ21+|c2|2ψ22++c∗2c1ψ2ψ1e+iE2ℏte−iE1ℏt++c∗1c2ψ1ψ2e+iE1ℏte−iE2ℏt.

No caso de c1 e c2 reais, a equação (6.63) se torna:

|Ψ(x,t)|2=|c1|2ψ21+|c2|2ψ22++c1c2ψ1ψ2(e+i(E2−E1)ℏt+e−i(E2−E1)ℏt).

Por fim, identificamos o termo entre os parênteses como uma função cosseno:

|Ψ(x,t)|2=|c1|2ψ21+|c2|2ψ22++2c1c2ψ1ψ2cos(E2−E1ℏt).

Chamando δE=E2−E1, concluímos que a densidade de probabilidade oscila com a frequência angular temporal:

ω=δEℏ.

Dizer que a densidade de probabilidade oscila com a frequência (6.66), é o mesmo que dizer que a densidade de probabilidade oscila com o período temporal:

2πδT=δEℏ.

E, a partir da equação (6.67), escrevemos:

δEδT=2πℏ.

∙  Finalmente chegamos ao título da seção!

A equação (6.68) é uma versão informal do principio da incerteza. Ela correlaciona a energia com o tempo. Em mecânica quântica, o tempo é um parâmetro usado para reger a evolução de variáveis dinâmicas (energia, posição e momento). O tempo não é uma variável dinâmica. Por isso, a relação que envolve tempo e energia não é considerada verdadeiramente um princípio de incerteza, pois correlaciona um parâmetro (o tempo) com uma variável dinâmica (a energia).

A resultado (6.68) basicamente nos diz que se o espaçamento energético δE é grande, o período de oscilação δT é pequeno, e vice-versa. Para chegar nele, partimos de (6.62), uma superposição de 2 autoestados. Ser δT pequeno, significa que a partícula muda muitas vezes de autoestado, oscila muitas vezes entre ψ1 e ψ2, e permanece pouco tempo em cada um desses autoestados. Em outras palavras, em uma superposição, se δE é grande, o tempo de vida de cada autoestado é pequeno. Por outro lado, se δE é pequeno, δT é grande, e a partícula muda poucas vezes de autoestado a cada segundo. Nesse caso, o tempo de vida do autoestado é grande. No limite, quando δE→0, ocorre δT→∞, e a partícula não muda mais de autoestado. Ela é levada a uma situação de energia única: E2→E1. Tirada da superposição, a partícula permanece apenas em um dos autoestado, o ψ1. Ali, pode ficar para sempre, pois o tempo de vida do autoestado numa situação em que não há superposição é infinito.

Como dissemos, (6.68) é uma versão do principio da incerteza, aplicada especificamente ao poço retangular infinito. Vendo de uma maneira mais ampla, ela pode ser ajustada para ter aspectos que reproduzam mais de perto a relação de Heisenberg [ seção 2.1 ]:

ΔEτ⩾ℏ2.

Na correlação da energia-tempo (6.69), ΔE é a própria incerteza na energia, todavia τ não é a incerteza no tempo. τ pode ser interpretado como tempo de vida de autoestado. Podemos relacionar τ com δT, lembrando que δT é o período temporal para ocorrer uma oscilação entre dois autoestados, sendo assim, a partícula deve permanecee em cada autoestado pelo tempo:

τ=δT2.

Levando (6.70) ao resultado (6.68) do poço infinito, encontramos:

ΔEτ=πℏ   (>ℏ2).

Como se vê, o poço retangular infinito, por meio do desfecho (6.71), satisfaz rigorosamente (6.69), o princípio da incerteza da energia-tempo.