Capítulo 8 A BARREIRA RETANGULAR

8.1 Introdução

A barreira retangular de potencial é caracterizada por ser descontinua em 2 pontos do espaço. Escolhemos a descontinuidade na origem e em $x = a$ :

$\begin{matrix} (8.1) & \begin{aligned} V (x) & = 0, & s e & x < 0, \\ = V_{0}, & s e & 0 ⩽ x ⩽ a, \\ = 0, & s e & x > a . \end{aligned} \end{matrix}$

Aqui, $V_{0}$ é uma grandeza positiva. Visualizamos a barreira retangular na Fig. 8.1.

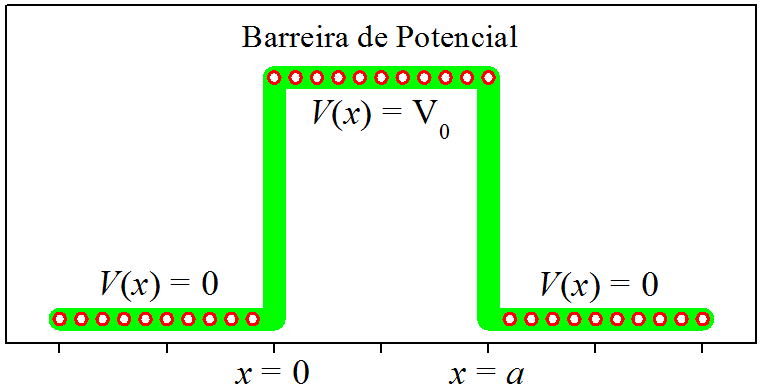
Figura 8.1: A barreira retangular de potencial.

Comparando com o degrau, que se se estende por todo semi-eixo positivo [ seção 7.1 ], a barreira atua somente em certa região do espaço. Os efeitos quânticos por ela manifestados, dependem da energia da partícula incidente. Na [ seção 8.2 ], estudaremos o caso da energia da partícula ser menor que a altura da bareira. Já na [ seção 8.3 ], trataremos o caso de $E$ ser maior que $V_{0}$ .

8.2 O regime de baixa energia

O regime de baixa energia é caracterizado por $E < V_{0}$ . A barreira divide o espaço em três regiões. Há a região de dentro ( $D$ ) e as regiões de fora ( $F$ ) da barreira. Em cada região, a solução da equação de Schrödinger apresenta uma peculiar expressão:

$\begin{matrix} (8.2) & \begin{aligned} ψ_{F} & = A e^{i k x} + B e^{- i k x}, & x < 0, \\ ψ_{D} & = C e^{i k_{D} x} + D e^{- i k_{D} x}, & 0 ⩽ x ⩽ a, \\ ψ_{F} & = F e^{i k x} + G e^{- i k x}, & x > a . \end{aligned} \end{matrix}$

Em cada região, o número de onda também apresenta uma peculiar expressão:

$\begin{matrix} (8.3) & \begin{aligned} k & = \frac{\sqrt{2 m E}}{ℏ}, & x < 0, \\ k_{D} & = \frac{\sqrt{2 m (E - V_{0})}}{ℏ}, & 0 ⩽ x ⩽ a, \\ k & = \frac{\sqrt{2 m E}}{ℏ}, & x > a . \end{aligned} \end{matrix}$

Por causa de $E < V_{0}$ , o número de onda dentro da barreira é imaginário. É favorável escrevê-lo na forma: $k_{D} = i q$ , onde $q$ é um número real e positivo:

$\begin{matrix} (8.4) & q = \frac{\sqrt{2 m (V_{0} - E)}}{ℏ} . \end{matrix}$

Após a transmissão através da barreira, não há motivos para a onda ser refletida, então podemos ajustar $G = 0$ . Ademais, substituindo (8.4) em (8.2), a solução da barreira retangular se escreve:

$\begin{matrix} (8.5) & \begin{aligned} ψ_{F} & = A e^{i k x} + B e^{- i k x}, & x < 0, \\ ψ_{D} & = C e^{- q x} + D e^{q x}, & 0 ⩽ x ⩽ a, \\ ψ_{F} & = F e^{i k x}, & x > a . \end{aligned} \end{matrix}$

Explorando (8.5), a onda de matéria incidente $A$ pode aparecer do outro lado da barreira, na forma da onda transmitida $F$ , ou aparecer na frente da barreira, na forma da onda refletida $B$ . Já dentro da barreira, ocorre certa “competição” entre as exponenciais reais $C$ e $D$ .

O módulo de $A$ , ao quadrado, é a probabilidade por unidade de comprimento que a partícula incidente “carrega” em direção à barreira. Analogamente, o módulo de $F$ , ao quadrado, é a probabilidade que a partícula transmitida “carrega” em direção ao infinito. Por causa da barreira, que dificulta a transmissão de probabilidades, $| F |^{2}$ nunca será maior que $| A |^{2}$ . O valor máximo que se pode atingir é $| F |^{2} = | A |^{2}$ . Então, para analisarmos a transmissão por uma barreira é útil estudarmos o comportamento da razão:

$\begin{matrix} (8.6) & T = \frac{| F |^{2}}{| A |^{2}} . \end{matrix}$

A razão (8.6) é adimensional e exprime a probabilidade de transmissão da partícula através da barreira. Ela é chamada de coeficiente de transmissão. Nosso trabalho agora será encontrar a expressão desse coeficiente. Podemos começar reescrevendo (8.6) na forma:

$\begin{matrix} (8.7) & \frac{1}{T} = \frac{A^{*} A}{F^{*} F} . \end{matrix}$

Segundo (8.7), nossa busca se resume em encontrar a expressão de $A / F$ . Para isso, podemos estabelecer as ligações entre as constantes complexas, $A$ , $B$ , $C$ , $D$ , e $F$ , por se valer das condições de continuidade da função de onda nas interfaces da barreira:

$\begin{matrix} (8.8) & I n t e r f a c e x = 0 {\begin{cases} ψ_{F} (0) = ψ_{D} (0) \\ \frac{d ψ_{F} (0)}{d x} = \frac{d ψ_{D} (0)}{d x} \end{cases} \end{matrix}$

$\begin{matrix} (8.9) & I n t e r f a c e x = a {\begin{cases} ψ_{D} (a) = ψ_{F} (a) \\ \frac{d ψ_{D} (a)}{d x} = \frac{d ψ_{F} (a)}{d x} \end{cases} \end{matrix}$

Resolvendo (8.8) e (8.9), encontramos:

$\begin{matrix} (8.10) & I n t e r f a c e x = 0 {\begin{cases} A + B = C + D \\ i k A - i k B = - q C + q D \end{cases} \end{matrix}$

$\begin{matrix} (8.11) & I n t e r f a c e x = a {\begin{cases} C e^{- q a} + D e^{q a} = F e^{i k a} \\ - q C e^{- q a} + q D e^{q a} = i k F e^{i k a} \end{cases} \end{matrix}$

Vamos trabalhar (8.11) duas vezes:

$1^{a} .$ Ao subtrair as equações, encontramos $C$ em função de $F$ :

$\begin{matrix} (8.12) & C = \frac{q - i k}{2 q} e^{q a} F e^{i k a} . \end{matrix}$

$2^{a} .$ Ao somar as equações, encontramos $D$ em função de $F$ :

$\begin{matrix} (8.13) & D = \frac{q + i k}{2 q} e^{- q a} F e^{i k a} . \end{matrix}$

Agora, eliminando o $B$ das equações (8.10), encontramos uma relação muito útil, que vai nos auxiliar a atingir nosso objetivo:

$\begin{matrix} (8.14) & 2 i k A = D (q + i k) - C (q - i k) . \end{matrix}$

Substituindo (8.12) e (8.13) em (8.14), encontramos:

$\begin{matrix} (8.15) & 2 i k A = \frac{(q + i k)^{2}}{2 q} e^{- q a} F e^{i k a} - \frac{(q - i k)^{2}}{2 q} e^{q a} F e^{i k a} . \end{matrix}$

Pela primeira vez temos algo que relaciona A com F:

$\begin{matrix} (8.16) & \frac{A}{F} = \frac{(q + i k)^{2}}{4 i q k} e^{- q a} e^{i k a} - \frac{(q - i k)^{2}}{4 i q k} e^{q a} e^{i k a} . \end{matrix}$

Resolvendo os termos quadráticos de (8.16) e, em seguida, agrupando as exponenciais reais:

$\begin{matrix} (8.17) & \frac{A}{F} = \frac{1}{2} (e^{q a} + e^{- q a}) e^{i k a} - \frac{(q^{2} - k^{2})}{4 i q k} (e^{q a} - e^{- q a}) e^{i k a} . \end{matrix}$

Identificamos as relações trigonométricas:

$\begin{matrix} (8.18) & \begin{aligned} e^{q a} + e^{- q a} & = 2 c o s h (q a), \\ e^{q a} - e^{- q a} & = 2 s e n h (q a) . \end{aligned} \end{matrix}$

Substituindo (8.18) em (8.17), temos a relação que procurávamos:

$\begin{matrix} (8.19) & \frac{A}{F} = c o s h (q a) e^{i k a} - \frac{(q^{2} - k^{2})}{2 i q k} s e n h (q a) e^{i k a} . \end{matrix}$

Para encontrar o coeficiente de transmissão, há necessidade de fazer o complexo conjugado de (8.19):

$\begin{matrix} (8.20) & {(\frac{A}{F})}^{*} = c o s h (q a) e^{- i k a} + \frac{(q^{2} - k^{2})}{2 i q k} s e n h (q a) e^{- i k a} . \end{matrix}$

Enfim, podemos determinar (8.7) através das relações (8.19) e (8.20):

$\begin{matrix} (8.21) & \frac{1}{T} = {c o s h}^{2} (q a) + \frac{{(q^{2} - k^{2})}^{2}}{4 q^{2} k^{2}} {s e n h}^{2} (q a) . \end{matrix}$

Lembrando que ${c o s h}^{2} (q a) = 1 + {s e n h}^{2} (q a)$ :

$\begin{matrix} (8.22) & \frac{1}{T} = 1 + [1 + \frac{{(q^{2} - k^{2})}^{2}}{4 q^{2} k^{2}}] {s e n h}^{2} (q a) . \end{matrix}$

Resolvendo os colchetes, chegamos à expressão final do coeficiente de transmissão para o caso do regime de $b$ aixa energia:

$\begin{matrix} (8.23) & \frac{1}{T_{b}} = 1 + \frac{{(k^{2} + q^{2})}^{2}}{4 k^{2} q^{2}} {s e n h}^{2} (q a) ._{} \end{matrix}$

8.3 O regime de alta energia

O regime de alta energia é caracterizado por $E > V_{0}$ . Seguindo a nomenclatura da [ seção 8.2 ], a solução da equação de Schrödinger por toda extensão da barreira retangular é:

$\begin{matrix} (8.24) & \begin{aligned} ψ_{F} & = A e^{i k x} + B e^{- i k x}, & x < 0, \\ ψ_{D} & = C e^{i k_{D} x} + D e^{- i k_{D} x}, & 0 ⩽ x ⩽ a, \\ ψ_{F} & = F e^{i k x}, & x > a . \end{aligned} \end{matrix}$

Em cada região, o número de onda também apresenta uma peculiar expressão:

$\begin{matrix} (8.25) & \begin{aligned} k & = \frac{\sqrt{2 m E}}{ℏ}, & x < 0, \\ k_{D} & = \frac{\sqrt{2 m (E - V_{0})}}{ℏ}, & 0 ⩽ x ⩽ a, \\ k & = \frac{\sqrt{2 m E}}{ℏ}, & x > a . \end{aligned} \end{matrix}$

Nosso objetivo aqui também é determinar o coeficiente de transmissão. Começamos aplicando as condições de continuidade das funções de onda nas interfaces da barreira:

$\begin{matrix} (8.26) & I n t e r f a c e x = 0 {\begin{cases} A + B = C + D \\ i k A - i k B = i k_{D} C - i k_{D} D \end{cases} \end{matrix}$

$\begin{matrix} (8.27) & I n t e r f a c e x = a {\begin{cases} C e^{i k_{D} a} + D e^{- i k_{D} a} = F e^{i k a} \\ i k_{D} C e^{i k_{D} a} - i k_{D} D e^{- i k_{D} a} = i k F e^{i k a} \end{cases} \end{matrix}$

Ao compararmos as equações (8.26) e (8.27) com as correspondentes da [ seção 8.2 ], fica evidente que a única diferença entre elas é a permuta:

$\begin{matrix} (8.28) & q ⟺ - i k_{D} . \end{matrix}$

Assim, a única coisa a fazer é fazer a permuta (8.28) na expressão final do coeficiente de transmissão deduzido na [ seção 8.2 ]:

$\begin{matrix} (8.29) & \frac{1}{T_{b}} = 1 + \frac{{(k^{2} + q^{2})}^{2}}{4 k^{2} q^{2}} {s e n h}^{2} (q a), \end{matrix}$

$\begin{matrix} (8.30) & \frac{1}{T} = 1 + \frac{{(k^{2} + [- i k_{D}]^{2})}^{2}}{4 k^{2} [- i k_{D}]^{2}} {s e n h}^{2} ([- i k_{D}] a) . \end{matrix}$

Cabe a recordação:

$\begin{matrix} (8.31) & {s e n h}^{2} (\pm i k x) = - {s e n}^{2} (k x) . \end{matrix}$

Substituindo (8.31) em (8.30), chegamoas à expressão final do coeficiente de transmissão para o caso do regime de $a$ lta energia:

$\begin{matrix} (8.32) & \frac{1}{T_{a}} = 1 + \frac{{(k^{2} - k_{D}^{2})}^{2}}{4 k^{2} k_{D}^{2}} {s e n}^{2} (k_{D} a) . \end{matrix}$

8.4 Um exemplo numérico

Estamos com as ferramentas preparadas para estudar a transmissão em barreiras de potencial. Analisaremos um elétron incidindo em uma barreira de altura $V_{0} = 200 m e V$ e espessura $a = 20 Å$ . Tomando como base a altura da barreira, dividimos a energia do elétron em dois intervalos: $0 < E < V_{0}$ [ $T_{b}$ , seção 8.2 ] e $V_{0} < E < 10 V_{0}$ [ $T_{a}$ , seção 8.3 ]. A Fig. 8.2 apresenta os gráficos dos coeficientes de transmissão $T_{b}$ e $T_{a}$ .

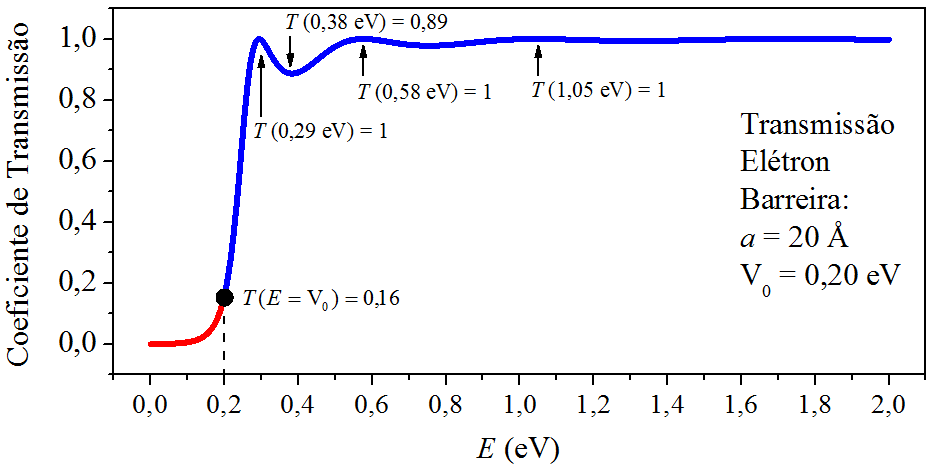
Figura 8.2: A transmissão por uma barreira retangular de potencial.

A Fig. 8.2 mostra alguns pontos em destaque. Existem energias especiais que proporcionam $T_{a} = 1$ , quer dizer, há 100% de chance da partícula ser transmitida através da barreira. A partícula “chega, e passa.” Isso ocorre nas energias $E = 290 m e V$ , $E = 580 m e V$ e $E = 1050 m e V$ . Vendo por outro ângulo, quer dizer que não há chance da partíula sofrer reflexão nas interfaces da barreira. Investigando a expressão do coeficiente de transmissão no regime de alta energia, a condição para $T_{a} = 1$ é $s e n (k_{D} a) = 0$ , ou seja:

$\begin{matrix} (8.33) & k_{D} = \frac{n π}{a}, n = 1, 2, 3... \end{matrix}$

Dentro da barreira, o número de onda é [ seção 8.3 ]:

$\begin{matrix} (8.34) & k_{D} = \frac{\sqrt{2 m (E - V_{0})}}{ℏ} . \end{matrix}$

Substituindo (8.33) em (8.34), encontramos a expressão das energias que geram 100% de transmissão:

$\begin{matrix} (8.35) & E_{n} = V_{0} + \frac{n^{2} π^{2} ℏ^{2}}{2 m a^{2}} . \end{matrix}$

As energias que condicionam transmissão máxima são chamadas de energias de ressonância da barreira. Nossa dedução mostra que a energia de ressonância é quantizada. Além disso, mostra que o termo que quantiza a expressão é idêntico à energia de confinamento de um poço retangular infinito, de largura igual à largura da barreira [ver seção 6.2 ].

Observando mais um pouco a Fig. 8.2, percebemos que muitas energias geram $T_{a} < 1$ . Por exemplo, $E = 380 m e V$ gera $T_{a} = 0, 89$ . Se há $89 %$ de chance da partícula ser transmitida através da barreira, também há $11 %$ dela ser refletida! Isso viola a visão clássica sobre o problema, que afirma que uma partícula tendo energia maior que uma barreira não poderia ser refletida por ela. De fato, na mecânica quântica:

$\begin{matrix} (8.36) & T + R = 1. \end{matrix}$

Onde $R$ é o coeficiente de reflexão.

A análise do regime de baixa energia, início da curva da Fig. 8.2, mostra que esse regime produz grande reflexão. Por exemplo, $E = 200 m e V$ gera $T_{b} = 0, 16$ , o que implica em $R_{b} = 0, 84$ . Se compararmos as probabilidades, agora a partícula tem mais chance de ser refletida do que transmitida. Mas ainda existe certa chance, mesmo que pequena, da partícula ser transmitida! Esse fato puramente quântico também abala a visão clássica do problema, que afirma que uma partícula com energia menor que uma barreira não poderia transpor esse potencial.

8.5 O tunelamento

A transmissão quântica por barreiras, quando a energia da partícula é menor que a energia potencial da barreira, é chamada de tunelamento. Dentro da barreira, ocorre interferência da onda $C$ , que caminha em direção à segunda interface $(x = a)$ , com a onda $D$ , que é refletida por essa interface. Mas, visto que o número de onda dessas ondas é imaginário, as exponenciais complexas se transformam em exponenciais reais.

Quando a interferência é pouco influenciada pela onda refletida, podemos modificar a expressão do coeficiente de transmissão $T_{b}$ , analisando algumas passagens da [ seção 8.2 ].

O que significa, em termos probabilísticos, a onda $D$ ser pouco influente? Quer dizer que ela carrega pouca probabilidade em relação à onda $C$ . Nesse sentido, podemos considerar que:

$\begin{matrix} (8.37) & | D |^{2} ≪ | C |^{2} . \end{matrix}$

Na [ seção 8.2 ], deduzimos as expressões das grandezas $C$ e $D$ . Aqui determinamos:

$\begin{matrix} (8.38) & \begin{aligned} | C |^{2} & = \frac{q^{2} + k^{2}}{4 q^{2}} | F |^{2} e^{2 q a}, \\ | D |^{2} & = \frac{q^{2} + k^{2}}{4 q^{2}} | F |^{2} e^{- 2 q a} . \end{aligned} \end{matrix}$

Logo,

$\begin{matrix} (8.39) & \frac{| D |^{2}}{| C |^{2}} = {(e^{- q a})}^{4} . \end{matrix}$

A condição (8.37) é seguramente satisfeita se $e^{- q a} ≪ 1$ . O que nos leva a seguinte aproximação:

$\begin{matrix} (8.40) & s e n h (q a) = \frac{e^{q a} - e^{- q a}}{2} ≅ \frac{e^{q a}}{2} . \end{matrix}$

Vamos utilizar (8.40) para encontrar um valor aproximado de $T_{b}$ :

$\begin{matrix} (8.41) & \frac{1}{T_{b}} = 1 + \frac{{(k^{2} + q^{2})}^{2}}{4 k^{2} q^{2}} {s e n h}^{2} (q a), \end{matrix}$

$\begin{matrix} (8.42) & \frac{1}{T_{b}} ≅ 1 + \frac{{(k^{2} + q^{2})}^{2}}{16 k^{2} q^{2}} e^{2 q a} . \end{matrix}$

Como $e^{2 q a} ≫ 1$ , o número “ $1$ ” que aparece em (8.42) pode ser desprezado, logo:

$\begin{matrix} (8.43) & T_{b} ≅ \frac{16 k^{2} q^{2}}{{(k^{2} + q^{2})}^{2}} e^{- 2 q a} . \end{matrix}$

Na próxima [ seção 8.6 ], vamos usar (8.43) para entender o funcionamento do Microscópio de Varredura por Tunelamento.

8.6 O STM

STM é a sigla de Scanning Tunneling Microscopy, Microscópio de Varredura por Tunelamento.

O STM se alicerça no fenômeno quântico do tunelamento. Quando a ponta metálica de um STM se aproxima de um material condutor (metal ou semicondutor dopado), entre a ponta e o condutor se forma uma barreira de potencia $V_{0}$ , de largura $a$ , igual à distância entre a ponta e o condutor. Pelo efeito de tunelamento, elétrons da ponta têm probabilidade de se transferirem para o condutor. A topografia da superfície do condutor pode ser mapeada fazendo a ponta do STM se movimentar sobre o condutor. Há dois modos de operação: o modo de altura constante e o modo de corrente constante. A Fig. 8.3 apresenta os detalhes desses modos de operação.

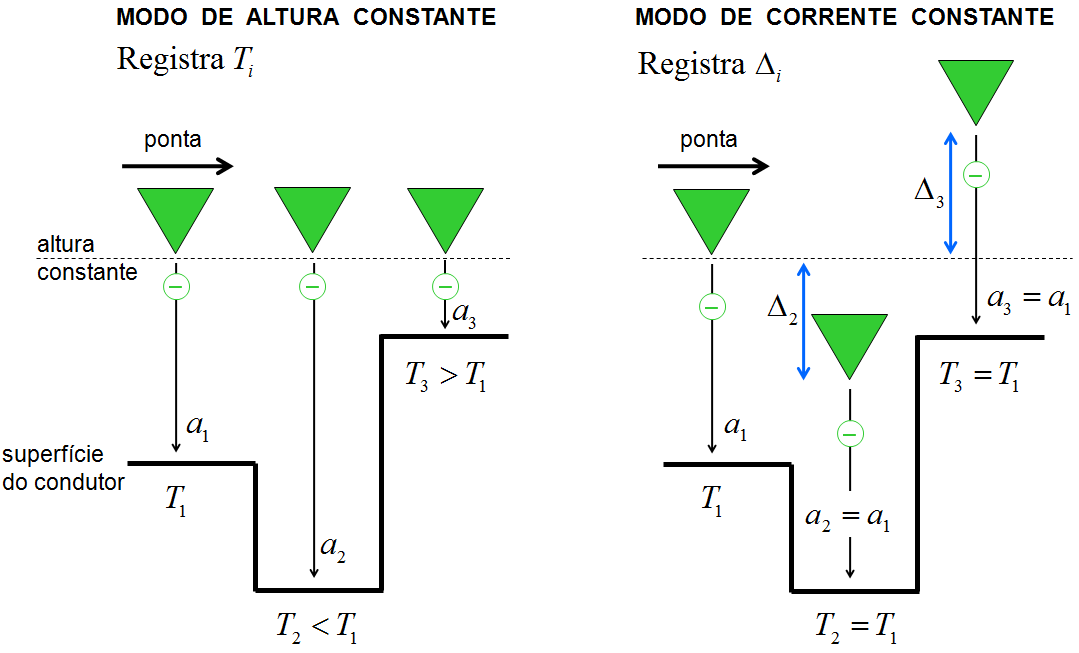
Figura 8.3: Os modos de operação de um STM.

No modo de altura constante, cada ponto sobre o condutor, de posição $x_{i}$ , forma uma barreira de largura $a_{i}$ , sendo $i = 1, 2, 3, e t c$ . Para cada $a_{i}$ , há uma probabilidade de tunelamento $T_{i}$ . Conforme vimos na [ seção 8.5 ], $T_{i} ≅ e^{- 2 q a_{i}}$ . Se há $N$ elétrons livres na ponta do microscópio, a quantidade $N T_{i}$ fará parte da corrente de tunelamento $I_{i}$ , ou seja, $I_{i} ≅ N T_{i}$ . Portanto, o STM vai registrar uma corrente de tunelamento diferente para cada ponto investigado. Ao traçar a corrente $I_{i}$ em função da posição da ponta sobre o condutor $x_{i}$ , teremos a imagem da superfície do material.

No modo de corrente constante, o registro é feito no deslocamento vertical da ponta do microscópio, indicado por $Δ$ na Fig. 8.3. No primeiro ponto em estudo, ajustamos a corrente base do processo: $I_{1}$ . Sabemos que a próxima corrente $I_{i}$ , depende de $T_{i}$ , que por sua vez, depende de $a_{i}$ . Ao fazer a varredura, podemos, então, ajustar $I_{i}$ para ter o mesmo valor da corrente base $I_{1}$ . Como fazemos isso? Liberando a ponta do microscópio para se movimentar na vertical. Portanto, o STM vai registrar um deslocamento vertical para cada ponto investigado. Ao desenhar $Δ_{i}$ em função de $x_{i}$ , veremos a imagem da superfície do material.

8.7 O fluxo de probabilidade pela barreira

Antes de avançar, seria importante recordar a nomenclatura utilizada para caracterizar a barreira retangular [ ver seção 8.2 ]. Como dissemos, a onda de matéria incidente $A$ pode aparecer do outro lado da barreira, na forma da onda transmitida $F$ , ou aparecer na frente da barreira, na forma da onda refletida $B$ .

A densidade de probabilidade do estado incidente $A$ , a grandeza $| A |^{2}$ , significa probabilidade por unidade de comprimento. Ela pode ser transformada em probabilidade por unidade de tempo, que chamaremos de fluxo de probabilidade $j_{A}$ . Para fazer a transformação, precisamos levar em conta a velocidade com que o estado $A$ avança em direção à barreira:

$\begin{matrix} (8.44) & v = \frac{ℏ k}{m} . \end{matrix}$

A transformação ocorre se definirmos:

$\begin{matrix} (8.45) & j_{A} = v | A |^{2} . \end{matrix}$

Lembrando que velocidade tem dimensão dada por comprimento $/$ tempo, fica claro que (8.45) tem dimensão de probabilidade $/$ tempo.

Vamos então listar todos fluxos de probabilidade que ocorrem na barreira retangular:

$\begin{aligned} (8.46) & j_{A} & = v | A |^{2}, \\ (8.47) & j_{B} & = - v | B |^{2}, \\ (8.48) & j_{F} & = v | F |^{2} . \end{aligned}$

Já falamos do fluxo de probabilidade incidente (8.46), mas também existe o fluxo de probabilidade refletica (8.47) e o fluxo de probabilidade transmitida (8.48). Fica claro que o fluxo total de entrada $(i n)$ e o fluxo total de saída $(o u t)$ , são:

$\begin{aligned} (8.49) & j_{i n} & = j_{A} + j_{B}, \\ (8.50) & j_{o u t} & = j_{F} . \end{aligned}$

Nesse novo alicerce teórico, o coeficiente de transmissão é definido como:

$\begin{matrix} (8.51) & T = \frac{j_{F}}{j_{A}} . \end{matrix}$

Substituindo (8.46) e (8.48) em (8.51), recuperamos o argumento usado na [ seção 8.2 ], quando dissemos que:

$\begin{matrix} (8.52) & T = \frac{| F |^{2}}{| A |^{2}} . \end{matrix}$

Assim como definimos o coeficiente (8.51), podemos definir o coeficiente de reflexão:

$\begin{matrix} (8.53) & R = \frac{- j_{B}}{j_{A}} ⟹ R = \frac{| B |^{2}}{| A |^{2}} . \end{matrix}$

Nota: Como o valor de (8.47) é negativo, há necessidade da inclusão do sinal $(-)$ , para fazer $R$ ser uma grandeza positiva.

Aqui vale ressaltar que $T + R = 1$ .

Agora, substituindo (8.53) em (8.49), e (8.51) em (8.50), encontramos:

$\begin{aligned} (8.54) & j_{i n} & = j_{A} (1 - R) = j_{A} T, \\ (8.55) & j_{o u t} & = j_{A} T . \end{aligned}$

Portanto, o fluxo total pela barreira é constante: $j_{o u t} = j_{i n}$ .

8.8 A origem do fluxo de probabilidade

Na [ seção 8.7 ], introduzimos a ideia de fluxo de probabilidade. Não nos preocupamos sobre sua origem. Agora vamos desenvolver a fórmulação que dá origem a esse fluxo.

Começamos multiplicando a equação de Schrödinger, equação (8.56), pelo complexo conjugado da função de onda:

$\begin{aligned} (8.56) & i ℏ \frac{\partial Ψ}{\partial t} & = - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} Ψ}{\partial x^{2}} + V Ψ, \\ (8.57) & i ℏ Ψ^{*} \frac{\partial Ψ}{\partial t} & = - \frac{ℏ^{2}}{2 m} Ψ^{*} \frac{\partial^{2} Ψ}{\partial x^{2}} + Ψ^{*} V Ψ . \end{aligned}$

Em seguida, multiplicamos o complexo conjugado da equação de Schrödinger, equação (8.58), pela função de onda:

$\begin{aligned} (8.58) & - i ℏ \frac{\partial Ψ^{*}}{\partial t} & = - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} Ψ^{*}}{\partial x^{2}} + V Ψ^{*}, \\ (8.59) & - i ℏ Ψ \frac{\partial Ψ^{*}}{\partial t} & = - \frac{ℏ^{2}}{2 m} Ψ \frac{\partial^{2} Ψ^{*}}{\partial x^{2}} + Ψ V Ψ^{*} . \end{aligned}$

Por fim, subtraímos os resultados (8.57) e (8.59):

$\begin{matrix} (8.60) & i ℏ (Ψ^{*} \frac{\partial Ψ}{\partial t} + Ψ \frac{\partial Ψ^{*}}{\partial t}) = - \frac{ℏ^{2}}{2 m} (Ψ^{*} \frac{\partial^{2} Ψ}{\partial x^{2}} + Ψ \frac{\partial^{2} Ψ^{*}}{\partial x^{2}}) . \end{matrix}$

Usando da matemática, os parênteses de (8.60) são:

$\begin{aligned} (8.61) & Ψ^{*} \frac{\partial Ψ}{\partial t} + Ψ \frac{\partial Ψ^{*}}{\partial t} & = \frac{\partial}{\partial t} (Ψ^{*} Ψ), \\ (8.62) & Ψ^{*} \frac{\partial^{2} Ψ}{\partial x^{2}} + Ψ \frac{\partial^{2} Ψ^{*}}{\partial x^{2}} & = \frac{\partial}{\partial x} (Ψ^{*} \frac{\partial Ψ}{\partial x} - Ψ \frac{\partial Ψ^{*}}{\partial x}) . \end{aligned}$

Utilizando (8.61) e (8.62) em (8.60), temos:

$\begin{matrix} (8.63) & \frac{\partial}{\partial t} (Ψ^{*} Ψ) = - \frac{\partial}{\partial x} [\frac{ℏ}{2 m i} (Ψ^{*} \frac{\partial Ψ}{\partial x} - Ψ \frac{\partial Ψ^{*}}{\partial x})] . \end{matrix}$

Observa-se que (8.63) relaciona a densidade de probabilidade, $ρ$ , com o fluxo de probabilidade, $j$ , onde:

$\begin{aligned} (8.64) & ρ & = Ψ^{*} Ψ, \\ (8.65) & j & = \frac{ℏ}{2 m i} (Ψ^{*} \frac{\partial Ψ}{\partial x} - Ψ \frac{\partial Ψ^{*}}{\partial x}) . \end{aligned}$

Logo, (8.63) pode ser escrita na forma compacta:

$\begin{matrix} (8.66) & \frac{\partial ρ}{\partial t} + \frac{\partial j}{\partial x} = 0. \end{matrix}$

A densidade de probabilidade e o fluxo de probabilidade estão interligados através da conhecida equação da continuidade, que surge no contexto da mecânica dos fluidos e também na eletrodinâmica clássica. Na mecânica dos fluidos, ela atesta em última análise a conservação da massa, e na eletrodinâmica, a conservação da carga. No presente contexto da mecânica quântica, ela reflete a conservação da probabilidade. Para entender melhor essa ideia, vamos fazer um jogo de palavras com as palavras probabilidade e elétrons:

“Num dado instante, e em num dado local, se o fluxo de entrada de elétrons for maior que o fluxo de saída, $\partial j / \partial x < 0$ , aumenta a concentração de elétrons desse local, $\partial ρ / \partial t > 0$ , mas, se o fluxo de entrada for igual ao fluxo de saída, $\partial j / \partial x = 0$ , a concentração de elétrons não se altera, $\partial ρ / \partial t = 0$ .”

Vamos calcular o fluxo de probabilidade do estado incidente $A$ :

$\begin{matrix} (8.67) & ψ_{A} = A e^{i k x} e^{\frac{- i E}{ℏ} t} ⟹ ψ_{A}^{*} = A^{*} e^{- i k x} e^{\frac{i E}{ℏ} t} . \end{matrix}$

Utilizando a definição (8.65) em (8.67), encontramos:

$\begin{matrix} (8.68) & \begin{aligned} j_{A} & = \frac{ℏ}{2 m i} (i k | A |^{2} + i k | A |^{2}) \\ = \frac{ℏ k}{m} | A |^{2} \\ = v | A |^{2} . \end{aligned} \end{matrix}$

O fluxo $j_{A}$ não depende da posição, $\partial j_{A} / \partial x = 0$ . Assim, a aquação de continuidade (8.66) implica em $\partial ρ_{A} / \partial t = 0$ , quer dizer, a densidade de probabilidade é constante. De fato, $ρ_{A} = | A |^{2}$ .

Nota: A barreira que estamos usando como ilustração é unidimensional. Assim, $ρ$ é probabilidade por comprimento. Isso leva $j$ a ser probabilidade por tempo. Porém, se o sistema fosse tridimensional, $ρ$ seria probabilidade por comprimento $^{3}$ . O que, por sua vez, levaria $j$ a ser probabilidade por (tempo $\cdot$ comprimento $^{2}$ ).

8.9 A normalização do inormalizável

Nem sei se a palavra $‘ ‘$ inormalizável $"$ será ou não incorporada aos dicionários. Mas sei que algumas funções de onda da mecânica quântica trazem em si o conceito de $‘ ‘$ aquilo que se não consegue normalizar $"$ . É o caso das ondas que caminham fora da barreira retangular [ seção 8.2 ], por exemplo, a onda incidente é representada por:

$\begin{matrix} (8.69) & ψ_{A} = A e^{i k x} ._{} \end{matrix}$

A normalização da função de onda (8.69) resulta em:

$\begin{matrix} (8.70) & \int_{- \infty}^{+ \infty} | ψ_{A} |^{2} d x = | A |^{2} \int_{- \infty}^{+ \infty} d x [r e s u l t a d o d i v e r g e n t e] . \end{matrix}$

Tais funções são características de estados não-ligados. Se uma função de onda representa um estado ligado, como as funções de onda do poço retangular infinito [ ver seção 6.2 ], então, quando fazemos a normalização, o resultado é finito.

Apesar da integral (8.70) divergir, ela é bem definida quando realizada em uma porção finita do espaço. Por exemplo, podemos fazer a integral considerando apenas certo comprimento $L = x_{2} - x_{1}$ , localizado na frente da barreira:

$\begin{matrix} (8.71) & \int_{x_{1}}^{x_{2}} | ψ_{A} |^{2} d x = | A |^{2} \int_{x_{1}}^{x_{2}} d x = | A |^{2} L [t o t a l d e p a r t í c u l a s] . \end{matrix}$

Se chamarmos, o total de partículas em $L$ de $N$ , então,

$\begin{matrix} (8.72) & n = \frac{N}{L}, \end{matrix}$

será a densidade de partículas incidentes, e, nesse caso:

$\begin{matrix} (8.73) & | A |^{2} = n . \end{matrix}$

Contornamos o problema da $‘ ‘$ inormalização $"$ . Agora somos capazes de dar condições de normalização ao problema dos estados não-ligados. Olhando para (8.73), se optarmos que a amplitude da onda incidente seja real, teremos $| A |^{2} = A^{2}$ , daí:

$\begin{matrix} (8.74) & A = \sqrt{n} . \end{matrix}$

Na [ seção 8.7 ], deduzimos que $| B |^{2} = R | A |^{2}$ e $| F |^{2} = T | A |^{2}$ , agora, com a dedução (8.73), podemos escrever:

$\begin{aligned} (8.75) & | B |^{2} = n R, ⟹ n_{R} = n R, \\ (8.76) & | F |^{2} = n T, ⟹ n_{T} = n T . \end{aligned}$

Portanto, ao definir que $| A |^{2}$ é igual a densidade de partículas incidentes, $| B |^{2}$ se torna igual à densidade de partículas refletidas, conforme (8.75), e $| F |^{2}$ se torna igual à densidade de partículas transmitidas, segundo (8.76)

Ademais, como não há criadouro ou sumidouro de partículas:

$\begin{matrix} (8.77) & n = n_{R} + n_{T} . \end{matrix}$

Trabalhar com grandezas ligadas à partícula parece mais intuitivo do que ligadas à probabilidade. De fato, para uma barreira exposta a um feixe de partículas incidentes $n$ , podemos usar a intuição e reescrever os fluxos de probabilidade, desenvolvidos na [ seção 8.7 ], em termos de fluxos de partículas:

$\begin{aligned} (8.78) & j_{A} & = v n & [f l u x o d e p a r t í c u l a s i n c i d e n t e s] \\ (8.79) & j_{B} & = - v n_{R} & [f l u x o d e p a r t í c u l a s r e f l e t i d a s] \\ (8.80) & j_{F} & = v n_{T} & [f l u x o d e p a r t í c u l a s t r a n s m i t i d a s] \\ (8.81) & j_{i n} & = v (n - n_{R}) & [f l u x o t o t a l n a e n t r a d a d a b a r r e i r a] \\ (8.82) & j_{o u t} & = v n_{T} & [f l u x o t o t a l n a s a í d a d a b a r r e i r a] \end{aligned}$

Ademais, também podemos reescrever os coeficientes de transmissão e de reflexão:

$\begin{aligned} (8.83) & T & = \frac{n_{T}}{n} & [c o e f i c i e n t e d e t r a n s m i s s ã o] \\ (8.84) & R & = \frac{n_{R}}{n} & [c o e f i c i e n t e d e r e f l e x ã o] \end{aligned}$