Capítulo 1 A NATUREZA TRAZ EM SI A PROBABILIDADE

1.1 Introdução

A experiência que revelou pela primeira vez o mundo quântico consiste em aquecer um corpo e fazer a leitura da intensidade e frequência da radiação eletromagnética que é produzida. No começo do aquecimento, o corpo não aparenta estar emitindo radiação, isso porque o infravermelho não se vê a olho nu. Depois, o corpo passa do vermelho para o amarelo e, em seguida, para o violeta, mostrando que grande parte da radiação emitida se concentrar na região visível do espectro eletromagnético. Com o aumento da temperatura, o corpo brilha com aparência esbranquiçada, indicando que agora grande parte da emissão é deslocada para além do espectro visível, se concentrando na região do ultravioleta. Enfim, conclui-se que o máximo da distribuição espectral se desloca em função da temperatura do corpo de acordo com a lei de deslocamento de Wien.

Além de emitir, um corpo também tem a capacidade de absorver e refletir a radiação eletromagnética. No caso ideal, podemos pensar em um corpo que não reflete radiação, assim, toda radiação que incide sobre esse corpo é absorvida. Tal corpo é chamado de corpo negro. A radiação emitida ou absorvida por um corpo negro é chamada radiação de corpo negro.

Usando argumentos da teoria clássica, tentou-se explicar a distribuição espectral da radiação de corpo negro. Em 1893, Wien deduziu uma lei que se ajustava a região de alta frequência, mas não explicava a região de baixa. Em 1900, Rayleigh e Jeans deduziram uma lei que se ajustava a região de baixa frequência, mas falhava notavelmente na região de alta.

Para ilustrar o que foi chamado de “catástrofe ultravioleta,” a Fig. 1.1 mostra a distribuição espectral da radiação de corpo negro para o caso da emissão estar ocorrendo à temperatura 10.000 K.

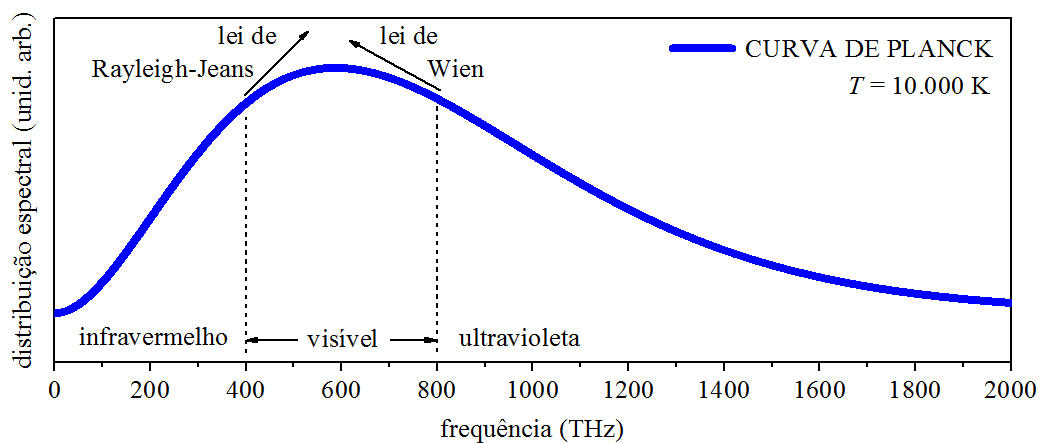
Figura 1.1: Radiação de corpo negro.

Max Planck se interessou pela catástrofe ultravioleta, em dezembro de 1900, ele propôs uma ideia revolucionária.

Quando um corpo absorve energia eletromagnética – ou de outra natureza, como a energia térmica –, uma hipótese aceita é que essa energia entra para aumentar o grau de agitação dos elétrons desse corpo, principalmente, dos elétrons da superfície, que passam a oscilar com frequência maior. Quando um corpo emite energia eletromagnética, diminui o grau de agitação desses elétrons, que passam a oscilar com frequência menor.

A questão é: qual a quantidade de energia que um oscilador pode absorver (emitir)? Antes de Planck, diziam que um oscilador poderia absorver (emitir) qualquer quantidade de energia, que a porção absorvida (emitida) não seguiria um padrão, diziam que a alteração da energia ocorria de maneira contínua.

Planck revolucionou dizendo que a porção de energia absorvida (emitida) por um oscilador segue um padrão: ser múltiplo inteiro da energia \(h\nu\) (\(h\) é uma constante que passou a ser chamada de constante de Planck e \(\nu\) representa frequência). Isso significa que um oscilador que absorve (emite) energia \(h\nu\), também pode absorver (emitir) energia \(2h\nu\), ou \(3h\nu\), ou, no caso geral, energia \(nh\nu\), onde \(n\) é um número inteiro. Assim, Planck afirmou que a alteração da energia ocorre de maneira descontínua. Assumindo que o nível de energia do oscilador é discreto, quantizado, e de maneira indireta, que a energia da radiação emitida por esse oscilador também é quantizada, Planck resolveu definitivamente o problema da catástrofe ultravioleta. Nasceu, assim, o mundo da energia quantizada. A nova teoria explicaria a distribuição espectral da radiação de corpo negro, como mostra a Fig. 1.1. Ajustando a lei de Planck com os dados experimentais, foi possível extrair o valor da sua constante universal, atualmente o valor aceito é \(h = 6,\!626 \times 10^{-34} \, {\rm Js}\).

A descontinuidade da energia mostrou ser o único caminho capaz de relacionar o mundo teórico com o mundo da natureza, e apesar disso, provocou muita desconfiança na comunidade científica da época, tanto que a maioria considerou a quantização da energia um capricho da imaginação, resultante de devaneios matemáticos. O próprio Planck, durante alguns anos, não percebeu o aspecto mais profundo de sua descoberta. Depois, sim! Pela descoberta da lei da radiação de corpo negro, Max Planck ganhou o prêmio Nobel em 1918.

Em 1905, Albert Einstein viu na quantização da energia da radiação de corpo negro base para desenvolver outra ideia revolucionária.

Naquela época, considerava-se a luz como onda eletromagnética, exclusivamente como onda. Já era fato comum que a incidência de luz sobre um metal liberava elétrons com certa velocidade. Se a luz fosse uma onda genuína, ao diminuir a sua intensidade, esperavam que os elétrons fossem “arrancados” com velocidade menor. Mas não é isso o que acontecia. Quando a intensidade luminosa diminuía, caia o número de elétrons liberados, mas eles eram liberados com a mesma velocidade.

Einstein compreendeu que a luz deveria ser uma partícula que transporta um quantum de energia \(h\nu\). Posteriormente, o quantum de luz passou a ser chamado de fóton.

Pensando a luz como partícula, se inicialmente um feixe de fótons \(h\nu\) incide sobre um metal e “arranca” elétrons com certa velocidade, ao diminuir a intensidade do feixe, o que acontece é a diminuição no número de fótons, mas eles continuam com a mesma energia, capazes de liberar elétrons com a mesma velocidade, porém em número menor. Por isso, são liberados menos elétrons do metal, mas a velocidade desses elétrons continua a mesma!

De acordo com Einstein, a luz que “arranca” elétrons de um metal é constituída por fótons de energia \(h\nu\), e a luz emitida pela matéria incandescente é constituída por fótons que possuem energia \(h\nu\) variada. Pela descoberta da lei do efeito fotoelétrico, Albert Einstein ganhou o prêmio Nobel em 1921.

Ao comparar as descobertas, Planck quantizou os níveis de energia dos osciladores do corpo negro, quando fez isso, indiretamente quantizou a energia da radiação de corpo negro. Falando dessa radiação, Planck não apresentou nova interpretação sobre sua natureza, no seu trabalho, ele considerou a radiação de corpo negro como onda eletromagnética. Em contraste, Einstein quantizou a própria energia da radiação eletromagnética. Ele argumentou que a quantização da energia da radiação de corpo negro é uma propriedade inerente da radiação de todo espectro eletromagnético. Ademais, Einstein forneceu nova interpretação à natureza da luz, no seu trabalho, ele considerou a luz como partícula (fóton).

– Foi assim que tudo começou…

No decorrer do livro, gradualmente vamos nos familiarizar com as “estranhezas” do mundo quântico, ser apresentados à teoria que narra o ambiente da escala atômica. Enquanto que a teoria clássica descreve o domínio macroscópico, vamos ver como a teoria quântica descreve o domínio microscópico. Atualmente podemos pensar o ambiente quântico “constituído apenas de ondas, constituído apenas de partículas, consistindo simultaneamente de ondas e partículas, ou como não consistindo de nada definido até que alguém o observe” – Osvaldo Pessoa Jr., Conceitos de Física Quântica (Editora Livraria da Física, 2003). As várias interpretações do mundo quântico se desenvolveram a partir da década de 20.

Niels Bohr, em 1927, ao analisar o comportamento dos fenômenos microscópicos, concebeu a interpretação da complementaridade: “Cada experimento envolvendo entidades microscópicas pode ser compreendido ou num quadro corpuscular (quando existem trajetórias bem definidas), ou num ondulatório (quando existem padrões de interferência), nunca ambos ao mesmo tempo.” Como exemplo de fenômeno ondulatório, podemos citar o padrão de interferência produzido por elétrons no experimento das duas fendas e, como exemplo de fenômeno corpuscular, o efeito fotoelétrico.

Max Born, também em 1927, percebendo que a natureza traz em si a probabilidade, concebeu uma interpretação probabilística à teoria quântica, algo que vamos elucidar na próxima seção analisando os resultados de uma experiência mental com carater quântico.

1.2 Uma interpretação probabilística à teoria quântica

\(\newcommand{\AA}{\unicode{xC5}}\) A experiência mental com carater quântico consiste em verificar a posição de um único elétron que se encontra em um trecho retilíneo de comprimento 100 \(\AA\). Tudo então é organizado para responder a pergunta: onde o elétron está? Para tornar a medida da posição praticável, detectores são espalhados pelos 100 \(\AA\), sendo cada detector responsável por cobrir a extensão de 20 \(\AA\).

A coleta de dados é sistemática: são realizadas 500 medidas, fundadas na seguinte suposição: após cada medição, as condições iniciais desse único elétron são restabelecidas. No decorrer da operação experimental, o número de vezes que o detector acusa a presença do elétron é anotado. Ao final das atividades, a contagem nos detectores apresentaria os resultados da Fig. 1.2.

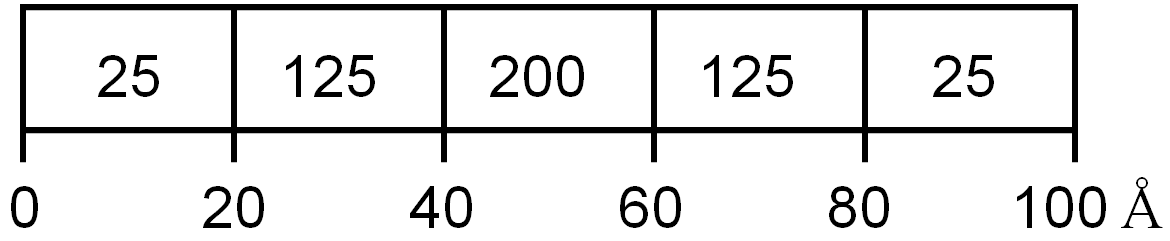
Figura 1.2: Resultados de uma experiência quântica.

Logo de cara verificamos que o elétron seria detectado em vários segmentos! Vamos transformar os números em porcentagens. Para isso, dividimos a contagem em cada detector pelo número total de medidas (500). A Fig. 1.3 mostra a distribuição de probabilidade ao longo dos 100 \(\AA\).

Figura 1.3: Distribuição de probabilidade.

Agora vamos supor a realização de outra medida, seria a de número 501. O que podemos dizer sobre a posição do elétron nessa nova medida? Pela análise da distribuição de probabilidade, poderíamos afirmar que a probabilidade do elétron ser encontrado nos segmentos \((0-20)\) e \((80-100)\) \(\AA\) é de apenas 5%; também que a maior probabilidade corresponderia ao segmento central, \((40-60)\) \(\AA\): 40%. Além disso, poderíamos dizer que há 90% de chance do elétron ser detectado no intervalo \((20-80)\) \(\AA\); e 10% fora dele.

Mas a questão crucial é: antes de realizarmos a medida – a próxima – de número 501, saberíamos dizer onde o elétron está? Será que ele estaria no segmento \((0-20)\) \(\AA\)? Ou no segmento \((40-60)\) \(\AA\)? Ou em qualquer outro? Em qual segmento o elétron se encontraria, antes da medida? – Não saberíamos a resposta: esta informação não está disponível!

Nossa experiência para responder a pergunta: “onde o elétron está?” mostra que há possibilidade dele ser detectado em qualquer segmento; nos oferece uma distribuição de probabilidade – somente!; aponta que só é possível afirmar onde o elétron está depois da medida – enquanto a medida não é realizada, ficamos apenas com a análise do conjunto de probabilidades. Nesse sentido, poderíamos dizer que, antes da medida, o elétron está qualquer lugar!

Agora vamos imaginar que “algo,” carregando uma fórmula que descrevesse o comportamento quântico do elétron, lhe entregasse a distribuição de probabilidade pronta! Sem dúvida ficaríamos motivados para conhecer a teoria por detrás de tal fórmula, a qual constrói curvas de probabilidade! Deter o conhecimento de tal teoria poderia ser muito vantajoso! Por exemplo, poderia nos poupar muito trabalho, pois, neste caso, não haveria necessidade de se fazer, primeiro, as 500 medidas, para, só depois, construirmos a distribuição de probabilidade. Mas a vantagem também poderia ser financeira, pois haveria muitos dispostos a pagar pelo conhecimento que descrevesse o comportamento quântico do elétron: valer-se de tal conhecimento poderia gerar uma nova tecnologia! Este “algo” é apresentado na equação (1.1).

\[ |\Psi(x,t)|^2 = \Psi^{\ast}(x,t) \Psi(x,t). \tag{1.1} \]

Aqui está a preciosa fórmula que constrói a distribuição de probabilidade e descreve o comportamento quântico de uma partícula. Na formulação da mecânica quântica, a função \(\Psi(x,t)\) é chamada função de onda. \(\Psi^{\ast}(x,t)\) representa o complexo conjugado de \(\Psi(x,t)\). E o produto da função de onda por seu complexo conjugado, \(\Psi^{\ast}(x,t)\Psi(x,t)\), é igual ao módulo ao quadrado da função de onda, \(|\Psi(x,t)|^2\).

Na interpretação probabilística desenvolvida por Max Born, a função de onda em si não tem caráter real e diretamente mensurável, podendo ser encarada como uma entidade sem realidade física, um artefato puramente matemático. É atribuída realidade física ao módulo ao quadrado da função de onda, cujo significado está ligado à presença de uma partícula através do espaço. Então, a coordenada x não representa um ponto de trajetória de uma partícula que se movimenta pelo espaço, mas, sim, uma possível posição dessa partícula no espaço. A interpretação probabilística abandonou o conceito de trajetória bem definida, o que adotou é o conceito de probabilidade de certa partícula estar em certa posição do espaço – probabilidade que emerge da equação (1.1).

A interpretação probabilística do módulo ao quadrado da função de onda se torna a ligação entre a teoria e a realidade. Mas, nesse contexto, o módulo ao quadrado não é probabilidade genuína, atenção!…, \(|\Psi(x,t)|^2\) é densidade de probabilidade. E, em situações unidimensionais, densidade de probabilidade é probabilidade por unidade de comprimento. Assim, a integral que aparece na equação (1.2) representa a probabilidade de uma partícula estar entre \(x=x_{1}\) e \(x=x_{2}\), no tempo em \(t\).

\[ \int_{x_1}^{x_2} |\Psi(x,t)|^2 \,\mathrm{d}x. \tag{1.2} \]

Voltando à nossa experiência que detecta elétrons, a probabilidade do elétron ser medido no segmento \((0-20)\) \(\AA\) seria calculada pela equação (1.3).

\[ \int_{0_{}}^{20 \AA} |\Psi(x,t)|^2 \,\mathrm{d}x = 0,\!05. \tag{1.3} \]

Já a equação (1.4), determinaria a probabilidade do elétron ser detectado no segmento \((40-60)\) \(\AA\). – E assim por diante!

\[ \int_{40_{\,} \AA}^{60 \, \AA} |\Psi(x,t)|^2 \, \mathrm{d}x = 0,\!40. \tag{1.4} \]

Montar e resolver as integrais que resultam em probabilidades depende do conhecimento prévio da função de onda, e assim, da formulação que gera \(\Psi(x,t)\). Isso quer dizer que precisamos nos habituar com uma equação diferencial desenvolvida por Erwin Schrödinger e tornada pública em 1926. Estudando a equação (1.5), nos familiarizaremos com a versão unidimensional da equação de Schrödinger.

\[ i \hbar \frac{\partial \Psi(x,t)}{\partial t} = -\frac{\hbar ^2}{2m}\frac{\partial ^2 \Psi(x,t)}{\partial x^2} + V(x,t)\Psi(x,t). \tag{1.5} \]

Nesta equação, \(V(x,t)\) é o potencial, de fato, a energia potencial que confina uma partícula de massa \(m\) numa região do espaço; e \(\hbar\) é a constante de Planck reduzida, ou seja, a constante de Planck dividida por \(2\pi\), por isso \(\hbar = 1,\!055 \times 10^{-34} \, {\rm Js}\).

O potencial vai assumir a forma do sistema em estudo. Por exemplo, se um elétron executa um movimento harmônico sob a ação de uma força restauradora \(F(x)=-kx\), o potencial assume a forma de uma parábola \(V(x)=kx^2/2\). Então, para encontrar \(\Psi(x,t)\) usando a equação (1.5), teríamos que resolver a equação diferencial (1.6).

\[ i \hbar \frac{\partial \Psi(x,t)}{\partial t} = -\frac{\hbar ^2}{2m}\frac{\partial ^2 \Psi(x,t)}{\partial x^2} + \frac{k x^2}{2} \Psi(x,t). \tag{1.6} \]

No decorrer do livro, resolveremos situações com potenciais que apresentam descontinuidades abruptas, chamados potenciais retangulares. Estes apresentam aspectos semelhantes ao poço de potencial mostrado na Fig. 1.4 o qual muda a pique nas posições \(x=0\) e \(x=a\).

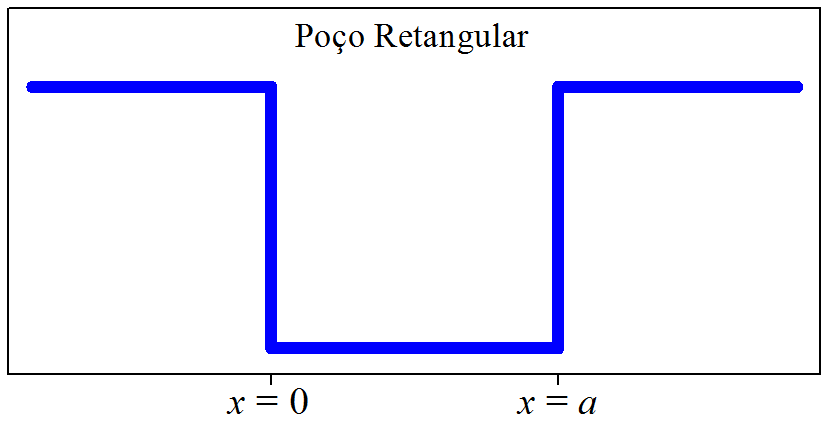
Figura 1.4: Potencial do tipo retangular.

Os potenciais do tipo retangular têm importância tanto no campo didático como no campo das aplicações, podendo ser utilizados como aproximações de sistemas físicos, químicos e biológicos. Nos últimos capítulos, vamos pôr em foco os semicondutores, por se tratar de uma área com grande impacto científico e tecnológico.

1.3 A equação de Schrödinger

São muitas as situações onde o potencial não depende do tempo, ou seja, \(V(x,t)=V(x)\). Nesse caso, podemos escrever a função de onda \(\Psi(x,t)\) como o produto de uma função \(\phi(t)\) que depende exclusivamente do tempo com outra função \(\psi(x)\) que depende exclusivamente da posição:

\[ \Psi(x,t) = \psi(x) \phi(t). \tag{1.7} \]

Considerando (1.7), a equação de Schrödinger [ seção 1.2 ] pode ser separada em duas equações.

A primeira equação é a equação temporal:

\[ \frac{\mathrm{d} \phi(t)}{\mathrm{d}t} = -\frac{iE}{\hbar} \phi(t). \tag{1.8} \]

E a segunda equação é a equação independente do tempo:

\[ -\frac{\hbar ^2}{2m}\frac{\mathrm{d} ^2 \psi(x)}{\mathrm{d} x^2} + V(x)\psi(x) = E \psi(x). \tag{1.9} \]

Onde a constante \(E\) é utilizada na separação de variáveis e tem dimensão de energia, portanto, significa a energia da partícula.

A equação temporal (1.8) tem solução trivial:

\[ \phi(t) = \mathrm{e}^{\large \frac{-iE}{\hbar} t}. \tag{1.10} \]

Por outro lado, a solução da equação independente do tempo (1.9) exige mais esforço e manipulações matemáticas, por causa da existência do potencial \(V(x)\). Todavia, após encontrada, a solução geral (1.7) terá o seguinte aspecto:

\[ \Psi(x,t) = \psi(x) \mathrm{e}^{\large \frac{-iE}{\hbar} t}. \tag{1.11} \]

Fica claro que \(|\Psi(x,t)|^2\) não depende do tempo, pois \(\mathrm{e}^{\large \frac{+iE}{\hbar} t} \mathrm{e}^{\large \frac{-iE}{\hbar} t} = 1\). Logo,

\[ |\Psi(x,t)|^2 = |\psi(x)|^2. \tag{1.12} \]

Apesar de \(\Psi(x,t)\) depender do tempo, \(|\Psi(x,t)|^2\) não muda com o passar do tempo, fazendo de \(\Psi(x,t)\) um estado estacionário. Isso significa que as quantidades que tem caráter puramente físico (real) ficam constantes no tempo: a probabilidade de encontrar uma partícula num segmento, o valor médio da posição de uma partícula, etc.

Há também ocasiões em que vamos nos deparar com um potencial constante em uma região do espaço, ou seja, \(V(x)=V_0\) (nesse livro \(V_0\) sempre representará potencial constante e positivo, quer dizer, \(V_0 > 0\)). Nesse caso, é conveniente rearranjar a equação de Schrödinger independente do tempo na seguinte forma:

\[ \frac{\mathrm{d}^2 \psi(x)}{\mathrm{d} x^2} = -\frac{2m(E-V_O)}{\hbar^2}\psi(x) = -k^2 \psi(x). \tag{1.13} \]

A constante \(k=\sqrt{2m(E-V_0)}/\hbar\) é chamada número de onda. Se a partícula tiver energia maior que o potencial, \(E>V_0\), o número de onda é real. Por outro lado, se \(E<V_0\), o número de onda é imaginário, como em \(k=iq\), onde \(q=\sqrt{2m(V_0-E)}/\hbar\).

Podemos nos perguntar olhando a equação diferencial logo acima: Qual é a função cuja derivada segunda resulta na própria função? Temos candidatas reais, \(\mathrm{cos}(kx)\) ou \(\mathrm{sen}(kx)\), mas também podemos pensar em uma solução complexa, do tipo:

\[ \psi(x) = A\mathrm{e}^{\large ikx} + B\mathrm{e}^{\large -ikx}. \tag{1.14} \]

Escolhendo a forma complexa, a função de onda geral fica da seguinte maneira:

\[ \Psi(x,t) = ( A\mathrm{e}^{\large ikx} + B\mathrm{e}^{\large -ikx} ) \mathrm{e}^{\large \frac{-iE}{\hbar}t}. \tag{1.15} \]

Quando \(E>V_0\), todos termos da função de onda (1.15) são complexos. Mas quando \(E<V_0\), ao sbstituir \(k=iq\), os termos entre parênteses se transformam em exponenciais reais, resultando em:

\[ \Psi(x,t) = ( A\mathrm{e}^{\large -qx} + B\mathrm{e}^{\large qx} ) \mathrm{e}^{\large \frac{-iE}{\hbar}t}. \tag{1.16} \]

1.4 O sentido de propagação da onda de matéria

A função de onda \(\Psi(x,t)\) que representa uma onda de matéria se propagando pelo espaço está vinculada ao caso \(E>V_0\), podendo ser reescrita como:

\[ \Psi(x,t)=A\mathrm{e}^{\large i(kx -\frac{E}{\hbar}t)} + B\mathrm{e}^{\large -i(kx +\frac{E}{\hbar}t)}. \tag{1.17} \]

Vamos examinar o sentido de propagação das ondas de amplitude \(A\) e \(B\) da equação (1.17). A parte real da onda \(A\) é \(\mathrm{cos}(kx -Et/\hbar)\). O máximo desse cosseno ocorre em \((kx -Et/\hbar)=0\), na posição \(x_A=(Et)/(k\hbar)\). Com o passar do tempo, \(x_A\) se desloca para a direita. Seguindo o mesmo raciocínio, a parte real da onda \(B\) tem máximo em \(x_B=-(Et)/(k\hbar)\). Com o passar do tempo, \(x_B\) se desloca para a esquerda. Portanto, a onda \(A\) se propaga para a direita e a onda \(B\) caminha para a esquerda, no decorrer do tempo.

1.5 Operações com números complexos

Há algo que vai nos acompanhar durante a leitura dos próximos capítulos: operações matemáticas com números complexos. Recordaremos duas operações que podem causar confusão por causa da semelhança da notação. Dado uma grandeza complexa \(z=a+bi\), sendo \(a\) e \(b\) reais, simbolizamos o módulo de \(z\) por \(|z|\). Daí, o módulo \(z\), ao quadrado, é determinado pela operação:

\[ |z|^2 = z^{\ast}z=(a-bi)(a+bi)=a^2+b^2. \tag{1.18} \]

Além do módulo de \(z\), ao quadrado, podemos pensar em fazer o próprio \(z\) ao quadrado, conforme:

\[ z^2 = zz=(a+bi)(a+bi)=a^2-b^2+2abi. \tag{1.19} \]

Logo, \(|z|^2 \neq z^2\). A igualdade \(|z|^2 = z^2\) só aconteceria se \(z\) fosse real, pois, se \(z=a\), temos \(|z|^2 = z^2 = a^2\).

1.6 O papel da função de energia potencial

Imagine uma carga \(q_M\) que se move em relação à outra carga \(q_F\) (que está fixa). Há um vínculo entre elas, pois podem se atraírem ou se repelirem através da força de Coulomb, de módulo:

\[ |\overrightarrow{F}| = \frac{1}{4 \pi \varepsilon} \frac{|q_M q_F|}{r^2}. \tag{1.20} \]

A energia potencial \(V\), de unidade \(\rm J\), descende dessa força. É associada ao estado de separação \(r\) entre as duas cargas \(q_M\) e \(q_M\). Dizemos que a carga móvel armazena energia potencial na posição que ocupa em relação à carga fixa. Nesse sentido, podemos falar sobre a “energia potencial da carga móvel.”

Quando \(q_M\) se desloca em relação à \(q_F\), por exemplo, entre as posições \(r_0 \longrightarrow r\), há variação na energia potencial \(\Delta V\), de valor igual ao trabalho \(W\) realizado pela força que \(q_F\) faz sobre \(q_M\) (mas com sinal oposto):

\[ \Delta V = V(r) - V(r_0) = - W. \tag{1.21} \]

Tomando o “zero” da energia potencial no infinito, quer dizer, fazendo \(V(\infty)=0\), e trazendo \(q_M\) do infinito, \(r_0=\infty\), chegamos à energia potencial da interação carga-carga (móvel-fixa):

\[ V_{M-F}(r) = - W_{}. \tag{1.22} \]

O cálculo do trabalho pode ser encontrado em livros de física básica, aqui vamos destacar o resultado de (\(-W\)):

\[ V_{M-F}(r) = q_M \phi_{F}(r)_{}. \tag{1.23} \]

Onde \(\phi_{F}(r)\), de unidade \(\rm J/C\), é o potencial gerado pela carga fixa \(q_F\):

\[ \phi_{F}(r) = \frac{1}{4 \pi \varepsilon} \frac{q_F}{r}. \tag{1.24} \]

Vamos exemplificar com a carga fixa sendo um elétron, \(q_F=-e\), gerando o potencial:

\[ \phi_{e}(r) = - \frac{1}{4 \pi \varepsilon} \frac{e}{r}_{}. \tag{1.25} \]

Vamos supor que a carga móvel também seja um elétron, \(q_M=-e\), então, a energia potencial da interação elétron-elétron (móvel-fixo) é:

\[ V_{e-e}(r) = \frac{1}{4 \pi \varepsilon} \frac{e^2}{r}_{}. \tag{1.26} \]

Os perfis das equações (1.25) e (1.26) são apresentados na Fig. 1.5.

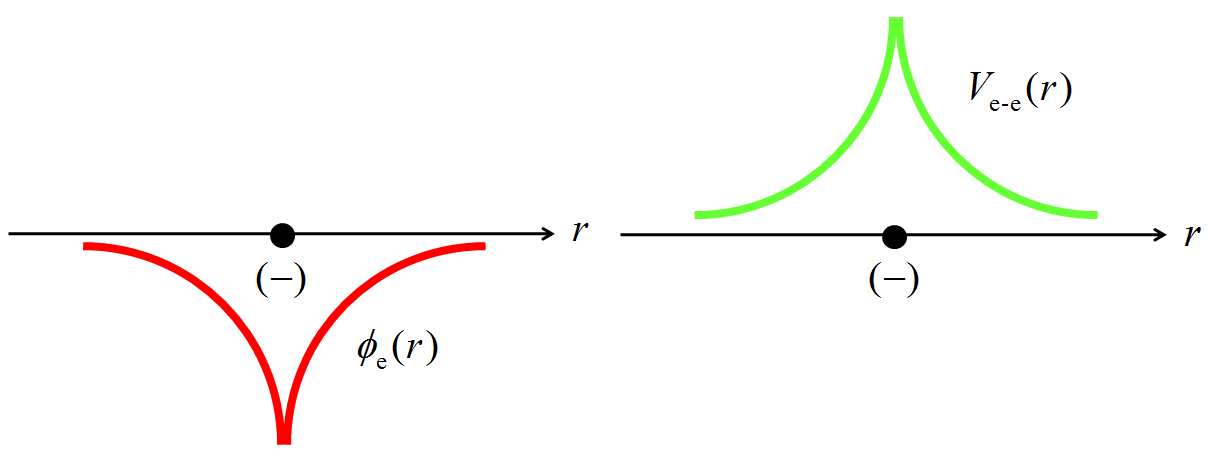
Figura 1.5: Perfis do potencial e da energia potencial da interação elétron-elétron, respectivamente.

O perfil da energia potencial (1.26), Fig. 1.5 (lado direito), mostra que quando o elétron móvel se afasta do fixo, sua energia potencial diminui, indicando, pela conservação da energia, que sua energia cinética aumenta. Como sabemos, cargas de mesmo sinal se repelem, então, o elétron móvel ganha energia cinética ao ser acelerado pelo elétron fixo.

Quando se trabalha com uma distribuição de cargas, de densidade volumétrica \(\rho\), de unidade \(\rm C/m^3\), é útil utilizar a equação de Poisson para determinar o potencial gerado por \(\rho\). Aqui apresentamos a equação de Poisson em uma dimensão e em coordenadas cartesianas:

\[ \frac{\mathrm{d} ^2 \phi_{\rho}(x)}{\mathrm{d} x^2} = - \frac{\rho}{\varepsilon}_{}. \tag{1.27} \]

Supondo \(\rho\) uniforme, independente de \(x\), a integração de (1.27) resulta em:

\[ \frac{\mathrm{d} \phi_{\rho}(x)}{\mathrm{d} x} = - \frac{\rho x}{\varepsilon}_{} + A. \tag{1.28} \]

Onde \(A\) é uma constante de integração. Agora, a integração de (1.28) resulta em:

\[ \phi_{\rho}(x) = - \frac{\rho x^2}{2 \varepsilon}_{} + Ax + B. \tag{1.29} \]

Onde \(B\) é outra constante de integração.

As constantes de integração podem ser determinadas por condições iniciais. Por exemplo, para encontrar \(A=0\), podemos fazer em (1.28):

\[ \frac{\mathrm{d} \phi_{\rho}(x=0)}{\mathrm{d} x} = 0_{}. \tag{1.30} \]

E para encontrar \(B\), podemos fazer \(\phi_{\rho}(x=\ell)=0\) em (1.29):

\[ B = - \frac{\rho \ell^2}{2 \varepsilon}. \tag{1.31} \]

Portanto, o potencial gerado pela distribuição uniforme de carga resulta em:

\[ \phi_{\rho}(x) = \frac{\rho}{2 \varepsilon}_{} (\ell^2 - x^2). \tag{1.32} \]

Se imaginarmos uma carga adicional \(q\), na presença da distribuição uniforme \(\rho\), a energia potencial da interação carga-distribuição (\(q-\rho\)) é:

\[ V_{q-\rho}(x) = \frac{q\rho}{2 \varepsilon}_{} (\ell^2 - x^2). \tag{1.33} \]

Vamos aplicar (1.32) e (1.33) para o caso de um elétron na presença de uma distribuição uniforme de elétrons, \(q=-e\) e \(\rho=-n_ee\), onde \(n_e\) é a densidade volumétrica de elétrons, de unidade \(\rm m^3\):

\[ \phi_{e}(x) = - \frac{n_ee}{2 \varepsilon} (\ell^2 - x^2). \tag{1.34} \]

\[ V_{e-e}(x) = \frac{n_ee^2}{2 \varepsilon} (\ell^2 - x^2). \tag{1.35} \]

Os aspectos gráficos das equações (1.34) e (1.35) são mostrados na Fig. 1.6.

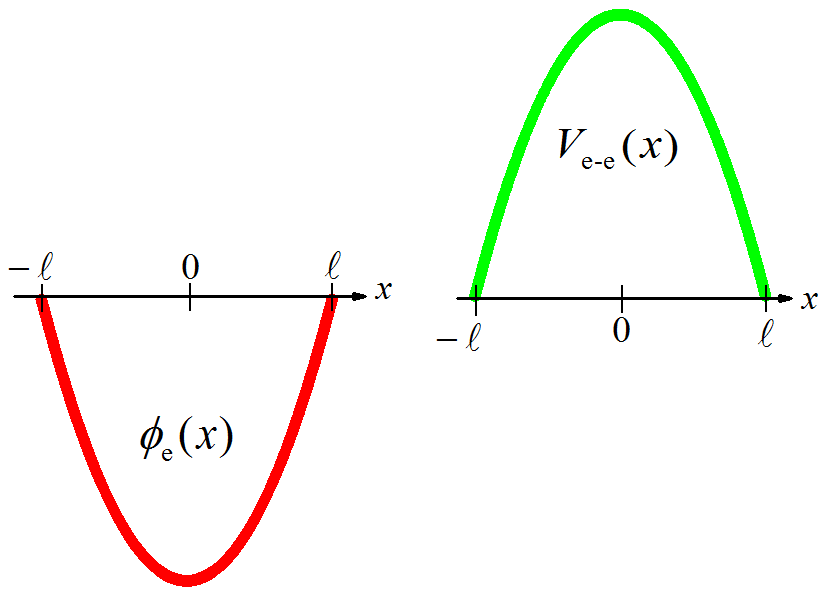
Figura 1.6: Perfis do potencial e da energia potencial da interação elétron-distribuição uniforme de elétrons, respectivamente.

Os aspectos gráficos do elétron que interage com uma distribuição de elétrons, Fig. 1.6, são semelhantes aos aspectos gráficos do elétron móvel que interage com o elétron fixo, Fig. 1.5. Isso ocorre por causa dos sinais das cargas, que são os mesmos nos dois casos. Logo, quando o elétron se aproxima da borda da distribuição de elétrons, \(x=\pm\ell\), sua energia potencial diminui, indicando que ele teve um aumento em sua energia cinética.

A força resultante que atua no elétron, devido aos elétrons da distribuição, pode ser determinada a partir da função de energia potencial:

\[ F = - \frac{\mathrm{d}V}{\mathrm{d}x}. \tag{1.36} \]

Substituindo o resultado (1.35) na definição (1.36), obtemos:

\[ F_{e-e}(x) = \frac{n_e e^2 x}{\varepsilon}. \tag{1.37} \]

Como se vê, a força (1.37) aponta para a borda da distribuição. Quando o elétron está em \(x>0\), a força aponta para a borda direita, \(x=+\ell\), acelerando o elétron nessa direção. Por outro lado, quando o elétron está na região \(x<0\), a força resultante aponta para a borda esquerda, \(x=-\ell\). Dessa forma, ao se movimentar em direção a uma das borda, o elétron aumenta sua energia cinética e diminui sua energia potencial.

Quando não há elétrons em um poço retangular \(V_0(x)\), o perfil de sua função de energia potencial é reto, mas, quando esse poço é ocupado por elétrons, o formato parabólico da interação elétron-elétron modifica o fundo do poço, sendo o poço resultante escrito como:

\[ V_R(x) = V_0(x) + V_{e-e}(x)_{}. \tag{1.38} \]

A Fig. 1.7 ilustra o preenchimento de um poço retangular com elétrons, conforme a equação (1.38).

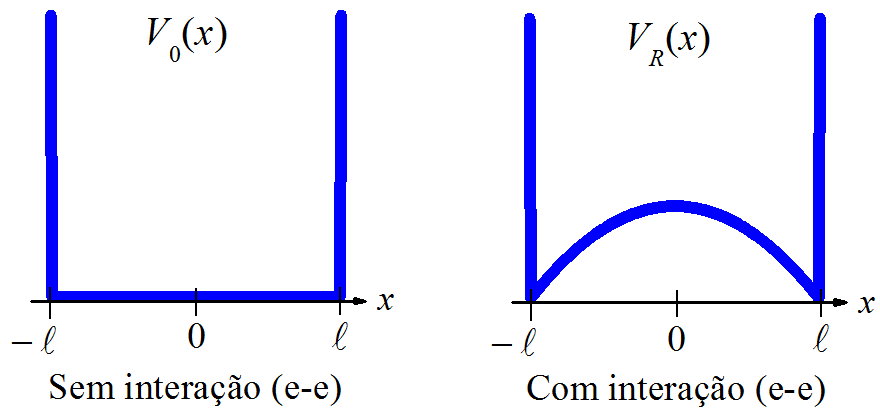
Figura 1.7: Perfis de um poço retangular vazio e outro com elétrons, respectivamente.

Foi mencionado que um campo de força descende da energia potencial, equação (1.36). Também já mensionamos que a equação de Schrödinger possui um termo relacionado com a energia potencial [ seção 1.2 ]. Isso quer dizer que resolver a equação de Schrödinger é resolver o problema de uma partícula sujeita a um campo de força, mas do ponto de vista quântico.

Tornamos este assunto mais explícito observando as derivadas da equação (1.38):

\[ \frac{\mathrm{d}V_R(x)}{\mathrm{d}x}=\frac{\mathrm{d}V_0(x)}{\mathrm{d}x}+\frac{\mathrm{d}V_{e-e}(x)}{\mathrm{d}x}_{}. \tag{1.39} \]

Como se vê, as derivadas (1.39) dão origem às seguintes forças:

\[ F_R(x) = F_0(x) + F_{e-e}(x)_{}. \tag{1.40} \]

As equações (1.39) e (1.40) nos dizem que o campo de força \(F_0\), gerado por \(V_0\), e o campo de força \(F_{e-e}\), gerado por \(V_{e-e}\), se somam para formar o campo de força resultante \(F_R\), gerado por \(V_R\).

Concluímos, então, o papel da função de energia potencial \(V_R\) na equação de Schrödinger: podemos afirmar que resolver a equação de Schrödinger com \(V_R\) é equivalente a resolver o problema quântico de uma partícula sujeita a um campo de força \(F_R\).