Capítulo 10 O POÇO RETANGULAR FINITO DE SEMICONDUTORES
10.1 Introdução
Até o momento, o livro não tratou de materiais. A partícula no poço retangular infinito, no degrau, na barreira e no poço retangular finito, estava no vácuo. Interagia com esses potenciais, mas ela mesmo não estava “mergulhada” em um material. Agora vamos introduzir os materiais. Escolhemos os semicondutores, por se tratar de um material amplamente utilizado na pesquisa e na indústria de alta tecnologia, como, por exemplo, na indústria de componentes semicondutores.
Nossa resolução de poços quânticos crescidos com materiais semicondutores se firma na aproximação da massa efetiva e na aproximação da função envelope. Os pormenores destas aproximações são apresentados em livros de Estado Sólido e Semicondutores. Lá, encontraremos que:
A aproximação da massa efetiva trabalha com uma primeira equação de Schrödinger para o elétron na banda de condução, uma segunda, para o buraco pesado na banda de valência e, uma terceira, para o buraco leve também na banda de valência.
A aproximação da função envelope trabalha com uma função que descreve a periodicidade do semicondutor, conhecida como função de Bloch, multiplicada por outra que descreve o confinamento do portador, conhecida como função envelope, isso, para construir a função de onda geral do portador no semicondutor.
10.2 A profundidade do poço
Em semicondutores, a profundidade do poço da banda de condução, que chamaremos de \(V_{0}^{\rm BC}\), é determinada através da energia da largura da faixa proibida (gap) do semicondutor que entra na composição do próprio poço e, também, por meio da energia do gap do semicondutor que forma as barreiras. Aqui, vamos chamar a energia do gap do poço de \(E_{g{\rm P}}\), e a energia do gap da barreira de \(E_{g{\rm B}}\).
Uma parte da diferença dos gaps, forma a profundidade do poço da banda de condução:
\[ V_{0}^{\rm BC} = Q \left( E_{g{\rm B}} - E_{g{\rm P}} \right). \tag{10.1} \]
O fator \(Q\) é empírico. Valores aceitáveis ficam ao redor de \(0,\!70\).
A outra parte da diferença dos gaps, forma a profundidade do poço da banda de valência, que chamaremos de \(V_{0}^{\rm BV}\):
\[ V_{0}^{\rm BV} = (1-Q) \left( E_{g{\rm B}} - E_{g{\rm P}} \right)._{} \tag{10.2} \]
\({\large \bullet \ }\) Um exemplo numérico.
Considere um poço retangular finito formado de barreiras de AlAs e poço de GaAs.
É aceitável, para esses semicondutores, os seguintes valores de gap:
\[\begin{align} E_{g{\rm B}}^{\rm AlAs} = 3,\!13\ {\rm eV}, \notag \\ \notag \\ E_{g{\rm P}}^{\rm GaAs} = 1,\!52\ {\rm eV}. \notag \end{align}\]
Supondo \(Q=0,\!76\), encontramos:
\[\begin{align} V_{0}^{\rm BC} = 1,\!22\ {\rm eV}, \notag \\ \notag \\ V_{0}^{\rm BV} = 0,\!39\ {\rm eV}. \notag \end{align}\]
10.3 A massa efetiva
O crescimento de um poço retangular finito utilizando semicondutores confina o elétron (\(e\)) na banda de condução, o buraco pesado (\(h\)) na banda de valência e o buraco leve (\(l\)) também na banda de valência. Então, o processo de obtenção das energias de confinamento e funções de onda desse poço quântico envolve três equações de Schrödinger:
Há uma equação para o elétron da banda de condução;
Outra, para o buraco pesado da banda de valência;
E uma terceira, para o buraco leve da banda de valência.
Na teoria dos semicondutores, as massas que entram nessas equações são chamadas de massas efetivas e são simbolizadas por \(m^*\). Os valores de \(m^*\) são impressos em relação à massa de repouso do elétron: \(m_0=9,\!11 \times 10^{-31}\ {\rm kg}\). Aqui, vamos utilizar os publicados por Landolt Börnstein, em Numerical Data and Functional Relationships in Science and Technology (New Series III/17a, Springer – Heidelberg, 1992). Como a lista de semicondutores é extensa, vamos nos prender aos semicondutores GaAs e AlAs.
| Portador | GaAs (\(m_0\)) | AlAs (\(m_0\)) |
|---|---|---|
| Elétron | 0,067 | 0,124 |
| Buraco leve | 0,087 | 0,260 |
| Buraco pesado | 0,475 | 0,500 |
Então, se resolvemos quanticamente um poço finito que foi crescido com barreiras de AlAs e poço de GaAs, será necessário usar 2 valores de massa efetiva para o poço da banda de condução e 4 valores para o poço da banda de valência.
| Massa efetiva | Representação e valor (\(m_0\)) |
|---|---|
| Elétron no poço | \(m^*_{e{\rm P}}=0,\!067\) |
| Elétron na barreira | \(m^*_{e{\rm B}}=0,\!124\) |
| Massa efetiva | Representação e valor (\(m_0\)) |
|---|---|
| Buraco leve no poço | \(m^*_{l{\rm P}}=0,\!087\) |
| Buraco leve na barreira | \(m^*_{l{\rm B}}=0,\!260\) |
| Buraco pesado no poço | \(m^*_{h{\rm P}}=0,\!475\) |
| Buraco pesado na barreira | \(m^*_{h{\rm B}}=0,\!500\) |
10.4 As condições de continuidade
As condições de continuidade da função de onda em semicondutores diferem do caso do elétron no vácuo [ seção 9.3 ]. Em toda extensão do poço retangular finito, o elétron no vácuo possui a mesma massa, sempre \(m_0=9,\!11 \times 10^{-31}\ {\rm kg}\). Já no poço crescido com semicondutores, a massa efetiva do portador no poço se distingue da massa efetiva do portador na barreira [ seção 10.3 ]. Isso faz com que as grandezas que caracterizam o poço dependam da massa efetiva local.
Vamos chamar a massa efetiva do portador (\(p\)) no poço de \(m^*_{p{\rm P}}\), e a massa efetiva do portador na barreira de \(m^*_{p{\rm B}}\). Com essa notação, assim ficam os números de onda na região do poço e das barreiras:
\[\begin{align} \newcommand{ \kP }{ k _ {\rm P} } \newcommand{ \PP }{ _ {\rm P} } \newcommand{ \BB }{ _ {\rm B} } \newcommand{ \mP }{ \dfrac {1} {m ^{\ast} _ {p{\rm P}}} } \newcommand{ \mB }{ \dfrac {1} {m ^{\ast} _ {p{\rm B}}} } \kP &=\frac{ \sqrt{2m^ * _ {p{\rm P}} \varepsilon} } {\hbar}, \tag{10.3}\\ \notag\\ q &=\frac{ \sqrt{2m^ * _ {p{\rm B}} (V_0 -\varepsilon)} } {\hbar}. \tag{10.4} \end{align}\]
Estando a interface poço-barreira localizada em \(x=\ell\), as condições de continuidade também passam a depender da massa efetiva local:
\[\begin{align} \psi \PP (\ell) &= \psi \BB (\ell), \tag{10.5}\\ \notag \\ \mP \frac{{\rm d}\psi\PP (\ell)} {{\rm d}x} &= \mB \frac{{\rm d}\psi\BB (\ell)} {{\rm d}x}. \tag{10.6} \end{align}\]
Vale a pena aplicar as condições (10.5) e (10.6) para o caso do elétron no vácuo:
\[\begin{align} \psi \PP (\ell) &= \psi \BB (\ell), \tag{10.7}\\ \notag \\ \frac{1}{m_0} \frac{{\rm d}\psi\PP (\ell)} {{\rm d}x} &= \frac{1}{m_0} \frac{{\rm d}\psi\BB (\ell)} {{\rm d}x}. \tag{10.8} \end{align}\]
Após o cancelamento das massas \(m_0\) que aparecem em (10.8), recuperamos as condições de continuidade apresentadas na [ seção 9.3 ].
10.5 As equações transcendentais
Na [ seção 9.3 ], deduzimos as equações transcendentais para o elétron no vácuo, utilizamos como ponto de partida, as condições de continuidade da função de onda. Na [ seção 10.4 ], comparamos as condições de continuidade do elétron no vácuo com as do portador no semicondutor. Foi observado uma única mudança. No caso do semicondutor, a condição de continuidade da derivada da função de onda é “ponderada” pelas massas efetivas locais:
\[ \newcommand{ \kP }{ k _ {\rm P} } \newcommand{ \PP }{ _ {\rm P} } \newcommand{ \BB }{ _ {\rm B} } \newcommand{ \mP }{ \dfrac {1} {m ^{\ast} _ {p{\rm P}}} } \newcommand{ \mB }{ \dfrac {1} {m ^{\ast} _ {p{\rm B}}} } {\rm Interface}\ x=0\ \left\{ \begin{array}{l} \mB \dfrac{\mathrm{d} \psi\BB(0)}{\mathrm{d}x} = \mP \dfrac{\mathrm{d} \psi\PP(0)}{\mathrm{d}x} \\ \mB \left( qB \right) = \mP \left( i\kP C - i\kP D \right) \end{array} \right. \tag{10.9} \]
\[ {\rm Interface}\ x=a\ \left\{ \begin{array}{l} \mP \dfrac{\mathrm{d} \psi\PP(a)}{\mathrm{d}x} = \mB \dfrac{\mathrm{d} \psi\BB(a)}{\mathrm{d}x} \\ \mP \left( i\kP C\,\mathrm{e}^{\large i\kP a} - i\kP D\,\mathrm{e}^{\large -i\kP a} \right) = \\ \ \ \ \ \ \ \ \ = \mB \left( -qF\,\mathrm{e}^{\large -qa} \right) \end{array} \right. \tag{10.10} \]
Rearranjando os resultados (10.9) e (10.10):
\[ {\small \left( q \times { m ^{\ast} _ {p{\rm P}} } \right) (B) = \left( \kP \times { m ^{\ast} _ {p{\rm B}} } \right) (iC - iD) } \tag{10.11} \]
\[ {\small \left( \kP \times { m ^{\ast} _ {p{\rm B}} } \right) \left( iC\,\mathrm{e}^{\large i\kP a} - iD\,\mathrm{e}^{\large -i\kP a} \right) = \left( q \times { m ^{\ast} _ {p{\rm P}} } \right) \left( -F\,\mathrm{e}^{\large -qa} \right) } \tag{10.12} \]
Ao comparar as equações (10.11) e (10.12) com as correspondentes do elétron no vácuo [ seção 9.3 ], notamos que os fatores \((q)\) e \((\kP)\), presentes no vácuo, se modificaram para \((q \times m^{\ast}_{p{\rm P}})\) e \((\kP \times m^{\ast}_{p{\rm B}})\), no caso dos semicondutores.
Conclusão: As equações transcendentais que aparecem na [ seção 9.3.4 ] modificam para:
\[\begin{align} {\rm tg} \left( \frac{\kP a}{2} \right) &= \frac{q}{\kP } \times \frac{ m^{\ast} _ {p{\rm P}} } { m^{\ast} _ {p{\rm B}} }, \tag{10.13}\\ \\ {\rm cotg}\left( \frac{\kP a}{2} \right) &= - \frac{q}{\kP} \times \frac{ m^{\ast} _ {p{\rm P}} } { m^{\ast} _ {p{\rm B}} }. \tag{10.14} \end{align}\]
10.6 Um exemplo numérico
Considere um poço retangular finito, de largura \(a=100\ \unicode{xC5}\), crescido com barreiras de AlAs e poço de GaAs.
Para esses semicondutores, e supondo \(Q=0,\!76\), os valores da profundidade do poço da banda de condução e do poço da banda de valência foram calculados na [ seção 10.2 ].
Para o elétron na banda de condução, as equações transcendentais [ seção 10.5 ] são:
\[\begin{align} \newcommand{ \kP }{ k _ {\rm P} } \newcommand{ \eP }{ m^{\ast} _ {e{\rm P}} } \newcommand{ \eB }{ m^{\ast} _ {e{\rm B}} } \newcommand{ \hP }{ m^{\ast} _ {h{\rm P}} } \newcommand{ \hB }{ m^{\ast} _ {h{\rm B}} } \newcommand{ \lP }{ m^{\ast} _ {l{\rm P}} } \newcommand{ \lB }{ m^{\ast} _ {l{\rm B}} } {\rm tg} \left( \frac{\kP a}{2} \right) &= \dfrac{ \sqrt{2 \eB (V _ {0}^{\rm BC} - \varepsilon)} } { \sqrt{2 \eP \varepsilon} } \times \dfrac{\eP}{\eB}, \tag{10.15}\\ \notag \\ {\rm cotg}\left( \frac{\kP a}{2} \right) &= - \dfrac{ \sqrt{2 \eB (V _ {0}^{\rm BC} - \varepsilon)} } { \sqrt{2 \eP \varepsilon} } \times \dfrac{\eP}{\eB}. \tag{10.16} \end{align}\]
Onde as massas efetivas do GaAs e AlAs estão na [ seção 10.3 ], e as expressoes dos números de onda \(\kP\) e \(q\) aparecem na [ seção 10.4 ].
A Fig. 10.1 mostra as cuvas (10.15) e (10.16).
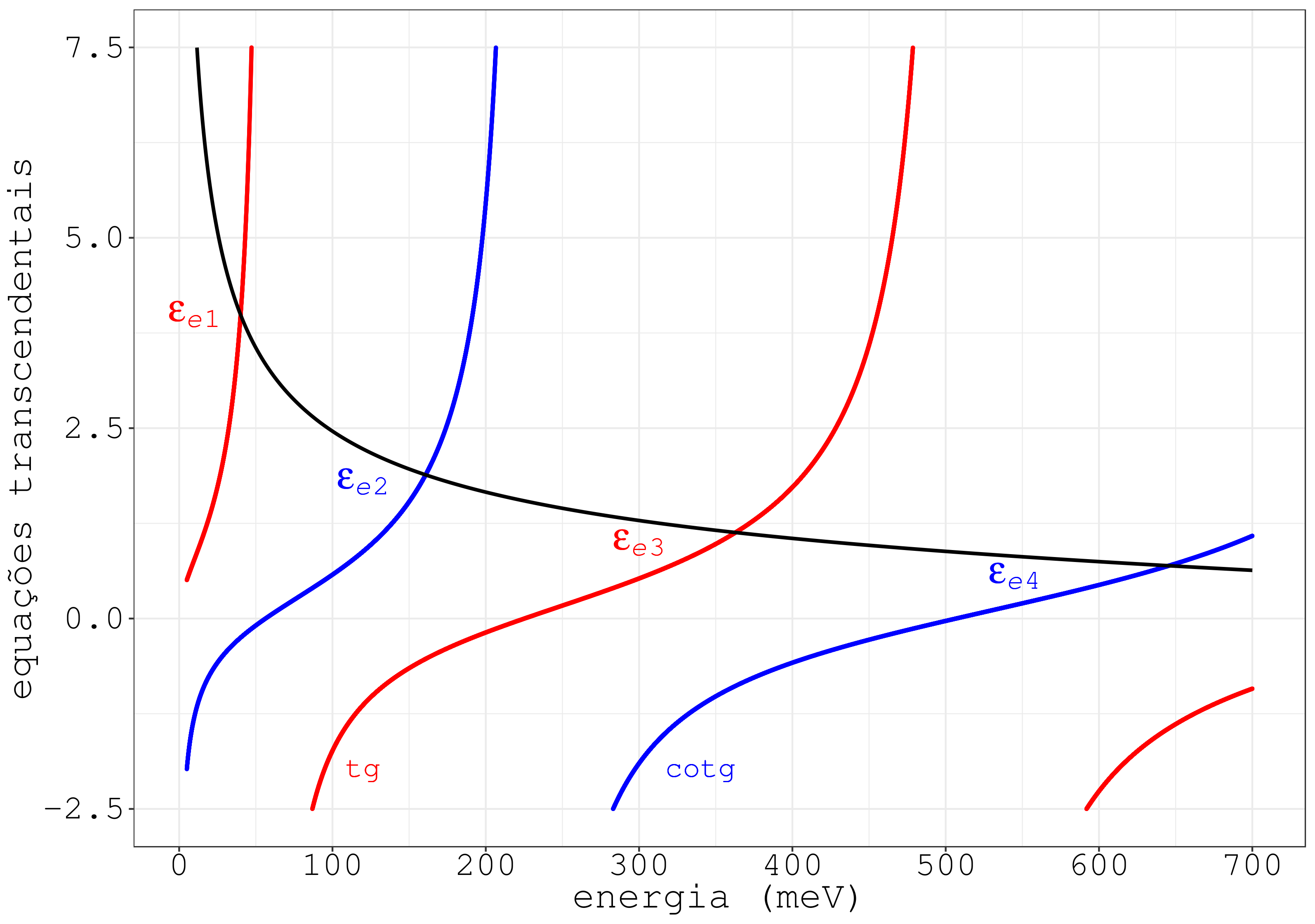
Figura 10.1: Equações transcendentais para o elétron no poço da banda de condução.
Já para o buraco pesado na banda de valência, as equações transcendentais são:
\[\begin{align} {\rm tg} \left( \frac{\kP a}{2} \right) &= \dfrac{ \sqrt{2 \hB (V _ {0}^{\rm BC} - \varepsilon)} } { \sqrt{2 \hP \varepsilon} } \times \dfrac{\hP}{\hB}, \tag{10.17}\\ \notag \\ {\rm cotg}\left( \frac{\kP a}{2} \right) &= - \dfrac{ \sqrt{2 \hB (V _ {0}^{\rm BC} - \varepsilon)} } { \sqrt{2 \hP \varepsilon} } \times \dfrac{\hP}{\hB}. \tag{10.18} \end{align}\]
A Fig. 10.2 mostra as cuvas (10.17) e (10.18).
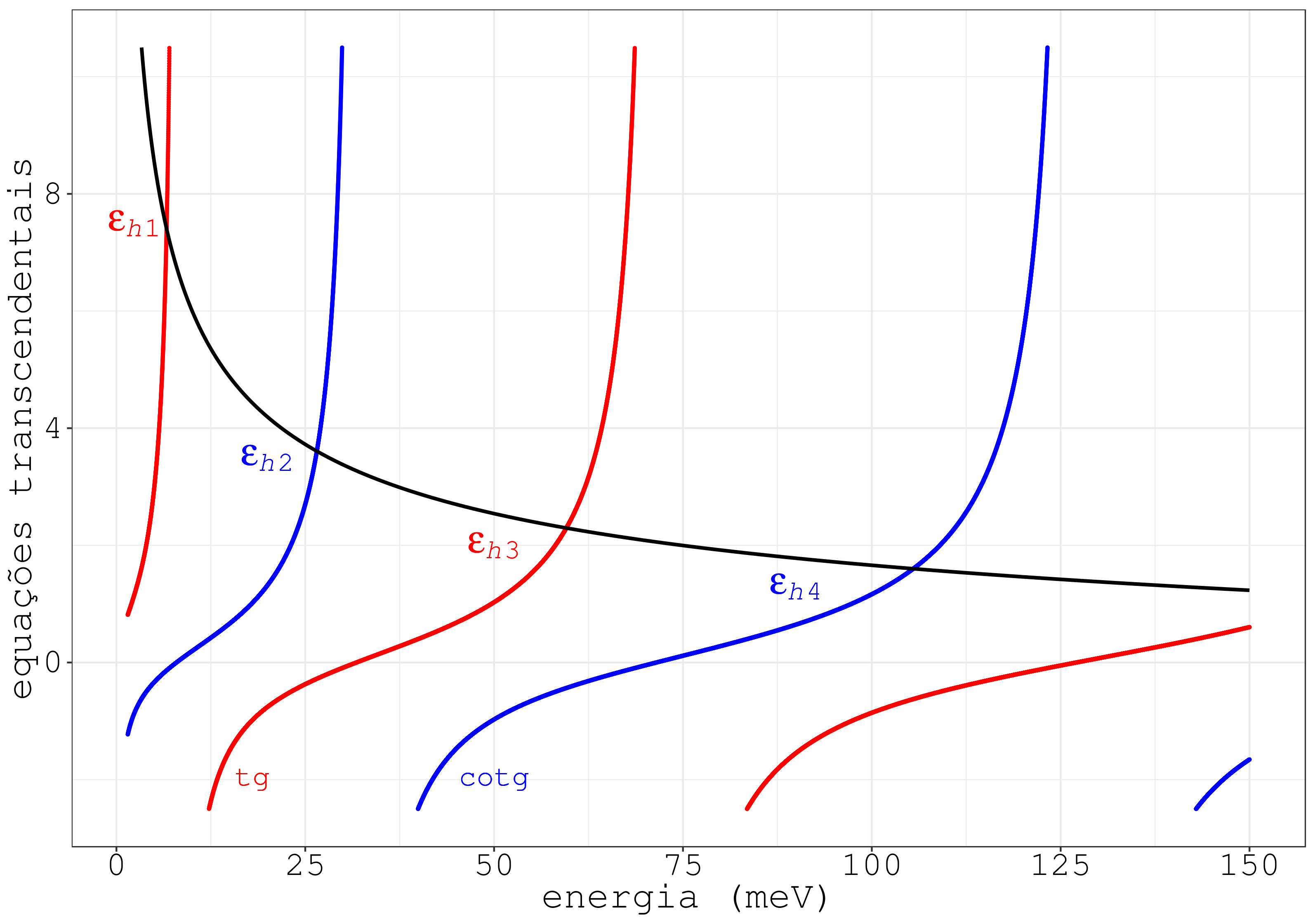
Figura 10.2: Equações transcendentais para o buraco pesado no poço da banda de valência.
E para o buraco leve também na banda de valência, as equações transcendentais são:
\[\begin{align} {\rm tg} \left( \frac{\kP a}{2} \right) &= \dfrac{ \sqrt{2 \lB (V _ {0}^{\rm BC} - \varepsilon)} } { \sqrt{2 \lP \varepsilon} } \times \dfrac{\lP}{\lB}, \tag{10.19}\\ \notag \\ {\rm cotg}\left( \frac{\kP a}{2} \right) &= - \dfrac{ \sqrt{2 \lB (V _ {0}^{\rm BC} - \varepsilon)} } { \sqrt{2 \lP \varepsilon} } \times \dfrac{\lP}{\lB}. \tag{10.20} \end{align}\]
A Fig. 10.3 mostra as cuvas (10.19) e (10.20).
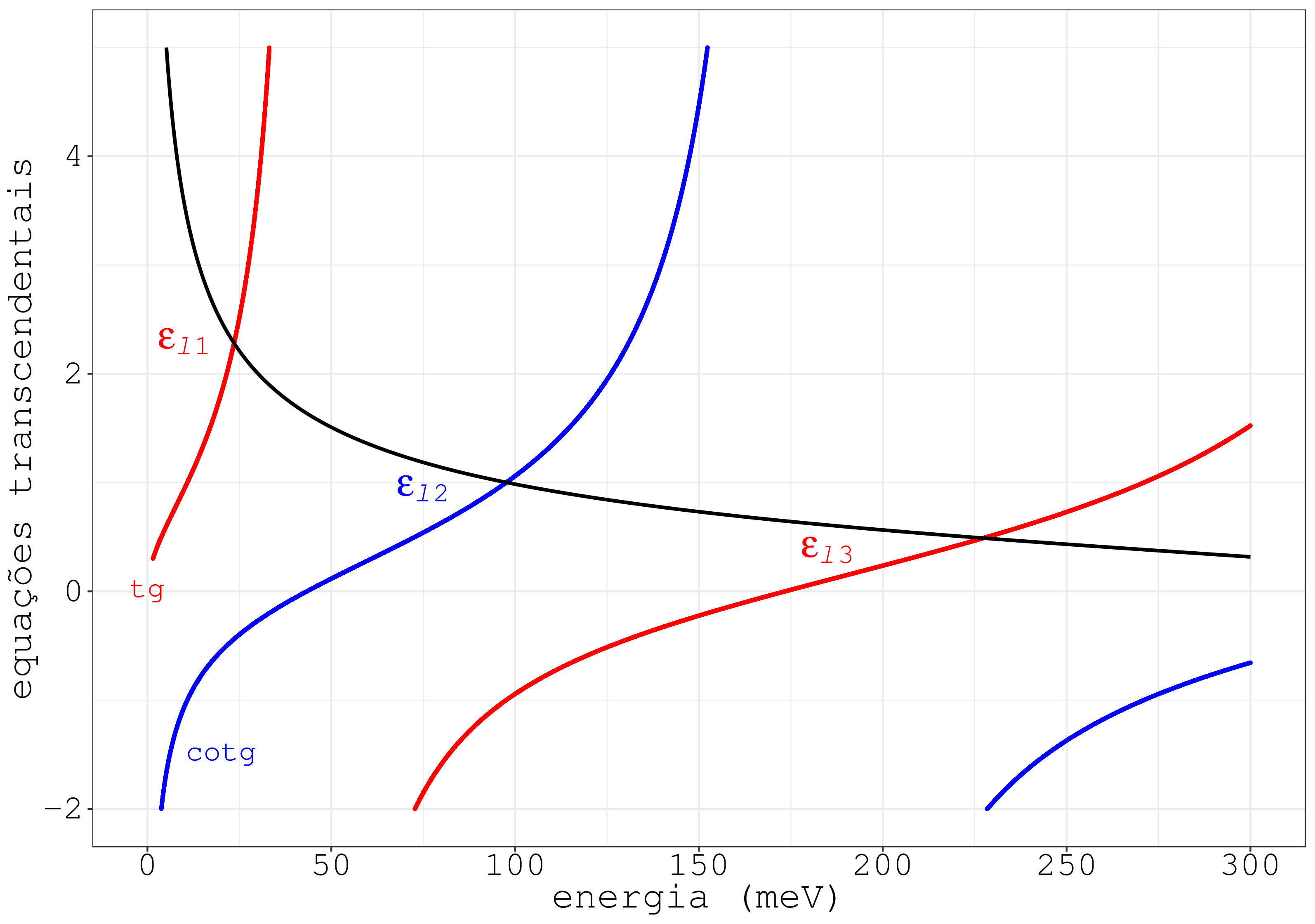
Figura 10.3: Equações transcendentais para o buraco leve no poço da banda de valência.
Resumimos, na tabela abaixo, os valores dos níveis de energia determinados pelas 3 figuras acima.
| Elétron (meV) | Buraco pesado (meV) | Buraco leve (meV) |
|---|---|---|
| \(\varepsilon _{e1}=40,\!1\) | \(\varepsilon _{h1}=6,\!7\) | \(\varepsilon _{l1}=23,\!6\) |
| \(\varepsilon _{e2}=160,\!8\) | \(\varepsilon _{h2}=26,\!5\) | \(\varepsilon _{l2}=97,\!6\) |
| \(\varepsilon _{e3}=363,\!0\) | \(\varepsilon _{h3}=59,\!6\) | \(\varepsilon _{l3}=227,\!3\) |
| \(\varepsilon _{e4}=645,\!6\) | \(\varepsilon _{h4}=105,\!5\) | |
A Fig. 10.4 síntetiza o exemplo. Ela é construída em escala, respeitando a proporção entre os valores que aparecem na tabela acima. São indicados os dois primeiros níveis de energia das bandas de condução e de valência, as profundidades dos poços e os valores dos gaps dos semicondutores GaAs e AlAs.
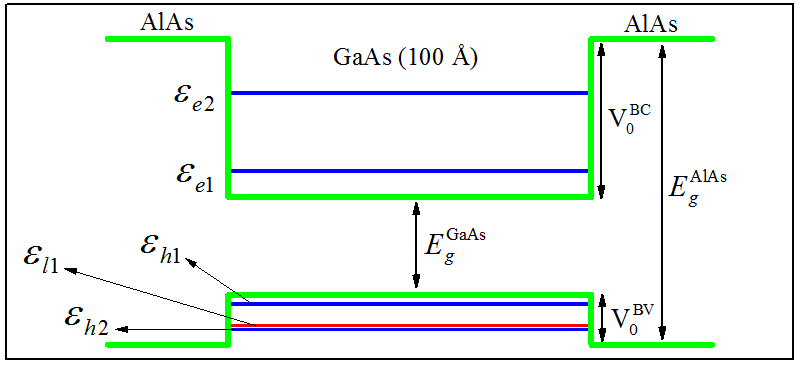
Figura 10.4: Níveis de energia do poço quântico de GaAs/AlAs.