Capítulo 4 A PARTÍCULA DELOCALIZADA E A LOCALIZADA

4.1 Introdução

Antes de tratarmos o assunto-título deste capítulo, vamos nos familiarizar com a equação de autovalor de um operador e com o princípio da superposição de ondas. Depois, agregaremos essas novas informações com os conceitos de probabilidade e incertezas para descrevermos o comportamento da partícula quântica totalmente localizada no espaço e da totalmente delocalizada.

4.2 A equação de autovalor

Em mecânica quântica, as grandezas físicas sujeitas à medição estão associadas a operadores matemáticos. Os operadores, por sua vez, operam sobre funções matemáticas alvos, instruindo que sejam realizadas algumas operações matemáticas específicas sobre essas funções. Por exemplo, a grandeza posição está associada ao operador da posição \(\widehat x\), e a grandeza momento linear associa-se ao operador do momento linear \(\widehat p\). O operador \(\widehat x\), instrui que a função alvo seja multiplicada por \(x\), enquanto que \(\widehat p\), instrui que realizemos a derivada da função alvo em relação à posição e, depois, multipliquemos o resultado por \(-i\hbar\), em suma:

\[ \widehat x = x. \tag{4.1} \]

\[ \widehat p = -i\hbar \frac{\mathrm{d}}{\mathrm{d}x}. \tag{4.2} \]

A medição de uma grandeza física, feita em certa experiência, resulta em uma quantidade numérica, mas vinculada à respectiva unidade da grandeza. Por exemplo, a medição da posição de uma partícula resulta em \(x\) \(\left( \mathrm{m} \right)\); já a medição do momento em \(\hbar k\) \(\left( \mathrm{ Js\cdot m^{-1} } \right)\). Aqui, o número de onda angular \(k\) está associado ao comprimento de onda \(\lambda\), através da relação:

\[ k = \frac{2\pi}{\lambda}. \tag{4.3} \]

Na teoria quântica, os resultados da medição de uma grandeza física que está associada a um operador \(\widehat A\), são os autovalores \(a\) que satisfazem a equação de autovalor:

\[ \widehat A \psi_a = a \psi_a. \tag{4.4} \]

Então, os resultados da medição da posição de uma partícula são os autovalores \(x\) \(\left( \mathrm{m} \right)\) que satisfazem a equação:

\[ \widehat x \psi_x = x \psi_x. \tag{4.5} \]

Já os resultados da medição do momento da partícula são os autovalores \(\hbar k\) \(\left( \mathrm{ Js\cdot m^{-1} } \right)\) que tornam verdadeira a equação:

\[ \widehat p \psi_k = \hbar k \psi_k. \tag{4.6} \]

Em (4.4), a solução \(\psi_a\) é chamada autoestado de \(\widehat A\), que corresponde ao autovalor \(a\). Então em (4.5), a solução \(\psi_x\) é o autoestado de \(\widehat x\) correspondente ao autovalor \(x\) \(\left( \mathrm{m} \right)\). Já em (4.6), a função \(\psi_k\) é o autoestado de \(\widehat p\) correspondente ao autovalor \(\hbar k\) \(\left( \mathrm{ Js\cdot m^{-1} } \right)\).

Fica o desafio de resolvermos as equações (4.5) e (4.6)…

4.3 O princípio da superposição

Um operador \(\widehat A\) pode formar um conjunto discreto de autofunções e de autovalores, do tipo:

\[ \widehat A \psi_1 = a_1 \psi_1 \\ \widehat A \psi_2 = a_2 \psi_2 \\ \widehat A \psi_3 = a_3 \psi_3 \\ \vdots \tag{4.7} \]

A base discreta de autoestados \(\left( \psi_1,\, \psi_2,\, \psi_3,\, ... \right)\), pode ser utilizada para decompor um estado quântico de uma partícula:

\[ \begin{aligned} \Psi(x) &= b_1\psi_1(x) + b_2\psi_2(x) + b_3\psi_3(x) +... \\ &= \sum_{i} b_i\psi_i(x) . \end{aligned} \tag{4.8} \]

Dizemos, então, que \(\Psi(x)\) é constituído por uma superposição linear dos autoestados de \(\widehat A\). Os coeficientes \(b_i\) são números complexos. Se forem efetuadas medições da grandeza física associada ao \(\widehat A\), a quantidade real \(b_i^{\ast}b_i\) será a probabilidade do autovalor \(a_i\) ser o resultado dessa medição; também é a probabilidade do autoestado \(\psi_i(x)\) ser o estado final dessa medição. A soma de todas as chances resulta em um, ou seja, \(\sum_{i} |b_i|^2=1\).

Vamos encontrar a expressão do coeficiente \(b_1\):

Primeiro, multiplicamos o \(\Psi\), da equação (4.8), pelo complexo conjugado de \(\psi_1\):

\[ \psi_1^{\ast}\Psi = b_1\psi_1^{\ast}\psi_1 + b_2\psi_1^{\ast}\psi_2 + b_3\psi_1^{\ast}\psi_3 +... \tag{4.9} \]

Em seguida, efetuamos a integração da equação (4.9) em todo espaço das posições:

\[ \begin{aligned} \int_{-\infty}^{+\infty} \psi_1^{\ast}\Psi \mathrm{d}x &= b_1 \int_{-\infty}^{+\infty} \psi_1^{\ast}\psi_1 \mathrm{d}x +\\ & +b_2 \int_{-\infty}^{+\infty} \psi_1^{\ast}\psi_2 \mathrm{d}x +\\ & +b_3 \int_{-\infty}^{+\infty} \psi_1^{\ast}\psi_3 \mathrm{d}x +... \end{aligned} \tag{4.10} \]

Neste ponto, precisamos lançar mão da ortogonalidade da base de autoestados:

\[ \begin{aligned} \int_{-\infty}^{+\infty} \psi_1^{\ast}\psi_1 \mathrm{d}x &= 1 \\ \int_{-\infty}^{+\infty} \psi_1^{\ast}\psi_2 \mathrm{d}x &= 0 \\ \int_{-\infty}^{+\infty} \psi_1^{\ast}\psi_3 \mathrm{d}x &= 0 \\ \vdots \end{aligned} \tag{4.11} \]

Por fim, aplicando (4.11) em (4.10), o coeficiente \(b_1\) resulta em:

\[ b_1 = \int_{-\infty}^{+\infty} \psi_1^{\ast}(x) \Psi(x) \mathrm{d}x. \tag{4.12} \]

Analogamente, a expressão de certo coeficiente \(b_i\) segue (4.12):

\[ b_i = \int_{-\infty}^{+\infty} \psi_i^{\ast}(x) \Psi(x) \mathrm{d}x. \tag{4.13} \]

Em (4.7), falamos de um operador que formar uma base discreta de autoestados, \(\psi_i(x)\), com \(i=1,\,2,\,3\,...\). Mas como proceder se certo operador formar uma base contínua de autoestados?

Vamos considerar o operador \(\widehat U\) formando uma base contínua de autoestados\(, \psi_u(x)\), sendo \(u\) um contínuo de reais, os autovalores desse operador. Seguindo o princípio da superposição em (4.8), a base contínua poderá ser utilizada para decompor um estado, mas, agora, ao invés de trabalharmos com somatórias, teremos que trabalhar com integrais:

\[ \Psi(x) = \int_{-\infty}^{+\infty} b(u) \psi_u(x) \mathrm{d}u. \tag{4.14} \]

Também, fazendo comparação com o caso discreto, equação (4.13), o coeficiente da superposição será assim determinado:

\[ b(u) = \int_{-\infty}^{+\infty} \psi_u^{\ast}(x) \Psi(x) \mathrm{d}x. \tag{4.15} \]

Agora, a quantidade \(b^{\ast}(u)b(u)\) não será uma probabilidade genuína, mas terá significado de densidade de probabilidade. A probabilidade genuína será \(|b(u)|^2\mathrm{d}u\), interpretada como a probabilidade de um resultado do experimento estar entre os autovalores \(u+\mathrm{d}u\). Desse modo, a probabilidade de um resultado do estar entre \(u_1 < u < u_2\), será:

\[ {\rm Pr}( u_1 < u < u_2 ) = \int_{u_1}^{u_2} |b(u)|^2\mathrm{d}u. \tag{4.16} \]

Lembrando da [ seção 1.2 ], podemos interpretar \(b(u)\) como certa função de onda do espaço \(u\), a qual gera certa densidade de probabilidade \(|b(u)|\).

4.4 A delta de Dirac

Antes de avançarmos na física, estamos recordando um pouco da matemática. Já falamos da equação de autovalor [ seção 4.2 ] e do princípio da superposição [ seção 4.3 ]. Agora vamos recordar alguma coisa sobre a delta de Dirac, muito utilizada no desenvolvimento da teoria quântica.

A delta de Dirac, centrada em \(x=\ell\), é definida como:

\[ \begin{aligned} \delta(x-\ell) &= \infty, \,\,\, & {\rm se} \,\,\, x = \ell ,\\ &= 0, \,\,\, & {\rm se} \,\,\, x \neq \ell . \end{aligned} \tag{4.17} \]

A Fig. 4.1 ilustra o perfil da \(\delta\)-Dirac centrada em \(x=25\); não é possível graficar o eixo \(y\) até o infinito, como exige (4.17), por isso devemos encarar a figura apenas como uma ilustração.

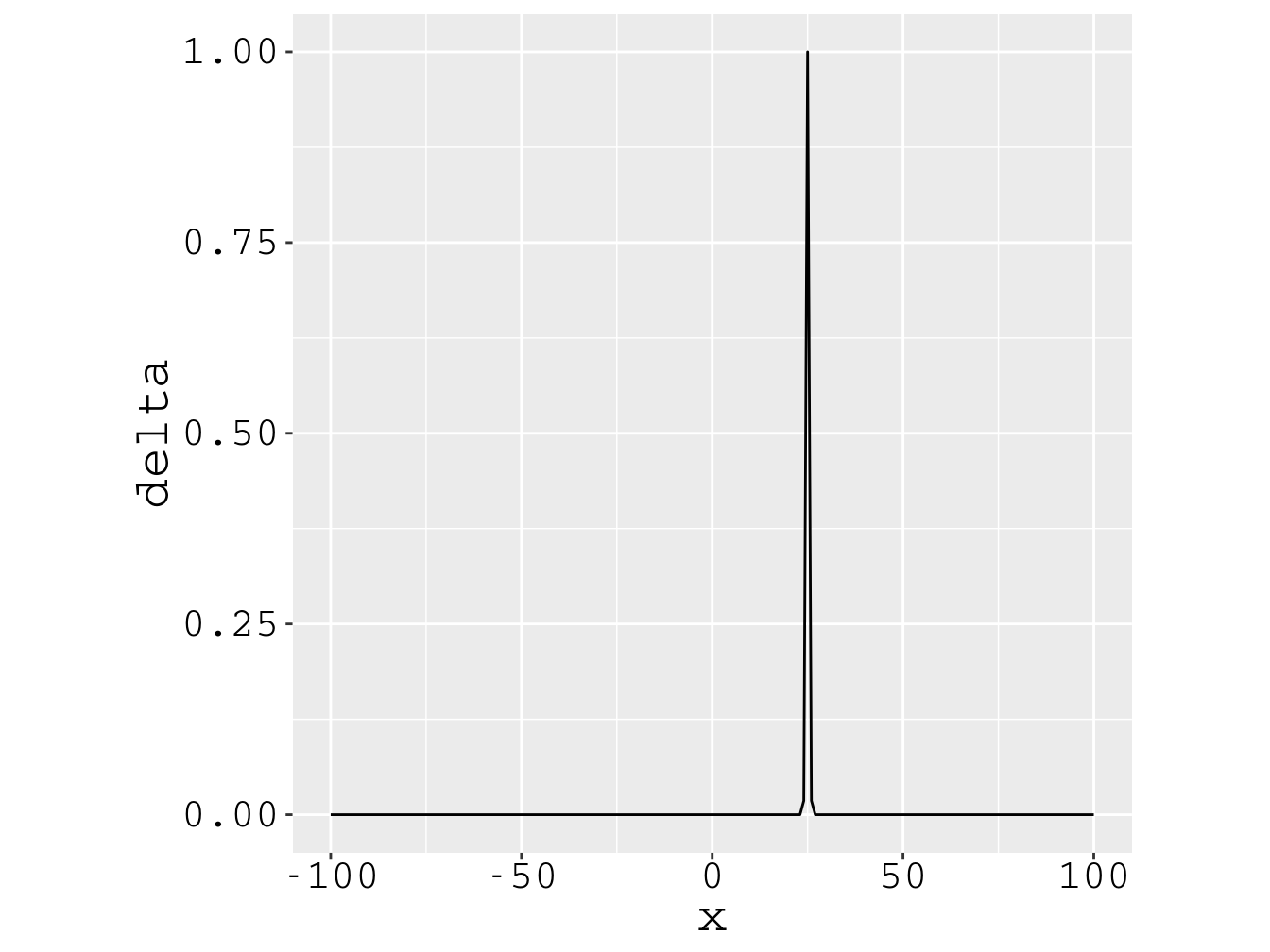
Figura 4.1: Ilustração de uma delta de Dirac centrada em \(x=25\).

A \(\delta\)-Dirac também pode ser representada no formato de integral de função exponencial:

\[ \delta(k-g) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} \mathrm{e}^{\large -i(k-g)x} \mathrm{d}x._{} \tag{4.18} \]

Uma propriedade importante da \(\delta\)-Dirac é chamada de filtragem-delta. Se \(F(x)\) for uma função contínua em torno da localização exata de uma delta de Dirac, então:

\[ \int_{-\infty}^{+\infty} F(x) \delta(x-\ell) \mathrm{d}x = F(\ell)._{} \tag{4.19} \]

Como se vê em (4.19), a delta de Dirac “percorre os valores da função e filtra apenas aquele que corresponde à localização exata dela.”

4.5 A partícula totalmente delocalizada

Vamos trabalhar a equação de autovalor do operador do momento linear [ seção 4.2 ]:

\[ \widehat p \psi_k(x) = \hbar k \psi_k(x). \tag{4.20} \]

Aplicando a instrução do operador do momento, ficamos com a seguinte equação diferencial:

\[ -i\hbar \frac{\mathrm{d}\psi_k(x)}{\mathrm{d}x} = \hbar k \psi_k(x). \tag{4.21} \]

O subscrito \(k\) que aparece em (4.21), subendende que cada autoestado \(\psi_k\) está associado a um autovalor \(\hbar k\) \(\left( \mathrm{ Js\cdot m^{-1} } \right)\), ademais, subentende que há um contínuo de autovalores \(\hbar k\), ou seja, \(-\infty < k < +\infty\).

A solução da equação (4.21) é trivial:

\[ \psi_k(x) = C\mathrm{e}^{\large ikx}. \tag{4.22} \]

A constante \(C\) deve ser encontrada pelo processo de normalização:

\[ \int_{-\infty}^{+\infty} |\psi_k(x)|^2 \mathrm{d}x = \int_{-\infty}^{+\infty} |C|^2 \mathrm{d}x._{} \tag{4.23} \]

Mas a equação (4.23) produz um resultado divergente. Então vamos determinar \(C\) analisando a integral (4.24), com o auxílio da delta de Dirac na forma exponencial [ seção 4.4 ]:

\[ \begin{aligned} \int_{-\infty}^{+\infty} \psi_k^{\ast}(x) \psi_g(x) \mathrm{d}x &= |C|^2 \int_{-\infty}^{+\infty} \mathrm{e}^{\large -i(k-g)x} \mathrm{d}x. \\ &= |C|^2 2\pi \delta(k-g). \end{aligned} \tag{4.24} \]

Justificamos a escolha \(|C|^2={2\pi}^{-1}\) para a integral (4.24) valer um delta de Dirac. Finalmente temos (4.22) normalizada:

\[ \psi_k(x) = \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large ikx}. \tag{4.25} \]

Como dissemos, a quantidade de autoestados do momento é infinita, em (4.25), \(k\) pode percorrer de \(-\infty\) até \(+\infty\). Vamos limitar nossa discussão a uma partícula preparada em um autoestado do momento, que chamaremos de estado \(\Psi_{\rm D}\), possuindo um único \(k\), por exemplo, \(k=g\):

\[ \Psi_{\rm D}(x) = \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large igx}._{} \tag{4.26} \]

A partir de (4.26), podemos determinar a densidade de probabilidade da posição:

\[ |\Psi_{\rm D}(x)|^2 = \frac{1}{2\pi} . \tag{4.27} \]

Para toda posição \(x\), a densidade de probabilidade (4.27) é constante. Isso quer dizer que a chance de a partícula ser encontrada em um intervalo infinitesimal em torno de \(x=\ell_1\), \(|\Psi_{\rm D}(\ell_1)|^2\mathrm{d}x\), é a mesma de ser encontrada em um intervalo infinitesimal em torno de \(x=\ell_2\), \(|\Psi_{\rm D}(\ell_2)|^2\mathrm{d}x\), e a assim por diante. A partícula \({\rm D}\), (4.26), tem posição totalmente incerta, \(\Delta x=\infty\). Dizemos que tal partícula está totalmente delocalizada – foi isso que motivou a escollha do subscrito \({\rm D}\). Visto que \(\Delta x=\infty\), temos \(\Delta p=0\), pelo princípio da incerteza [ seção 2.1 ]. Isso quer dizer que medições do momento sempre resultarão numa mesma medida, o autovalor \(\hbar g\) \(\left( \mathrm{ Js\cdot m^{-1} } \right)\). Dizemos que a partícula está num estado de momento certo.

Portanto, o que concluímos desta seção é que a partícula \({\rm D}\) possui momento certo e posição totalmente incerta.

4.6 A partícula totalmente localizada

Nosso objetivo agora é lidar com a equação de autovalor [ seção 4.2 ] do operador da posição [ \(\widehat x\) ]:

\[ \widehat x \psi_x(x) = x \psi_x(x). \tag{4.28} \]

Exclarecimento sobre a notação: em (4.28), \(x\) é coordenada (\(x\)), mas \(x\) também é autovalor de \(\widehat x\). Para fazer distinção, \(x\) continuará sendo coordenada (\(x\)), mas \(\ell\) passará a fazer o papel de autovalor de \(\widehat x\). Com este exclarecimento, a equação (4.28) muda para a forma:

\[ \widehat x \psi_\ell(x) = \ell \psi_\ell(x). \tag{4.29} \]

A solução da equação (4.29) pode ser deduzida a partir da filtragem-delta [ seção 4.4 ], pois:

\[ F(x) \delta(x-\ell) = F(\ell) \delta(x-\ell). \tag{4.30} \]

No nosso caso \(F(x)=x\), então, a equação (4.30) tem a forma:

\[ x \delta(x-\ell) = \ell \delta(x-\ell). \tag{4.31} \]

Vejam a semelhança entre as equações (4.29) e (4.31). Por isso concluímos que \(\psi_\ell\) é um delta de Dirac centrado em \(x=\ell\), ou seja:

\[ \psi_\ell(x) = \delta(x-\ell)._{} \tag{4.32} \]

O subscrito \(\ell\) subentende um contínuo de autovalores, onde cada autovalor \(\ell\) \(\left( \mathrm{m} \right)\) associa-se ao seu autoestado \(\psi_\ell\).

Como acabamos de dizer, a quantidade de autoestados da posição é infinita, em (4.32), \(\ell\) pode percorrer de \(-\infty\) até \(+\infty\). Vamos limitar nossa discussão a uma partícula preparada em um único autoestado da posição, possuindo um único autovalor \(\ell\):

\[ \Psi_{\rm L}(x) = \delta(x-\ell)._{} \tag{4.33} \]

A partir de (4.33), podemos determinar a densidade de probabilidade da posição:

\[ |\Psi_{\rm L}(x)|^2 = |\delta(x-\ell)|^2._{} \tag{4.34} \]

Levando em conta a definição da delta de Dirac [ seção 4.4 ], a equação (4.34) produz dois resultados:

\[ \begin{aligned} |\Psi_{\rm L}(x)|^2 &= \infty, \,\,\, & {\rm se} \,\,\, x = \ell_{} ,\\ &= 0, \,\,\, & {\rm se} \,\,\, x \neq \ell . \end{aligned} \tag{4.35} \]

Como se vê, não há chance da partícula \({\rm L}\), (4.33), ser encontrada fora da posição \(x=\ell\). Como era de se esperar, esta partícula só poderá ser achada em \(x=\ell\). Dizemos que esta partícula está num estado de posição certa, totalmente localizada – aqui está o porquê do subscrito \({\rm L}\). Sua incerteza na posição é zero, \(\Delta x=0\). Visto que \(\Delta x=0\), temos \(\Delta p=\infty\), pelo princípio da incerteza [ seção 2.1 ]. Isso quer dizer que medições do momento poderão resultar em qualquer medida dentre os autovalores \(-\infty < \hbar k< +\infty\).

Portanto, o que concluímos desta seção é que a partícula \({\rm L}\) possui posição certa e momento totalmente incerto; ver o contraste com a partícula \({\rm D}\) [ seção 4.5 ].

4.7 Mais sobre a partícula totalmente delocalizada

Na [ seção 4.5 ], batizamos a partícula totalmente delocalizada de partícula \({\rm D}\):

\[ \Psi_{\rm D}(x) = \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large igx}._{} \tag{4.36} \]

Entendemos que sua densidade de probabilidade da posição é constante:

\[ |\Psi_{\rm D}(x)|^2 = \frac{1}{2\pi}._{} \tag{4.37} \]

Entendemos, também, que seu momento é único, \(k=g\), mas que sua posição é totalmente incerta. Vamos explorar este fato. Por ter posição totalmente incerta, a partícula \({\rm D}\) está numa superposição [ seção 4.3 ] de autoestados [ \(\delta(x-\ell)\) ] do operador posição [ \(\widehat x\) ], simultaneamente centrada em todos autovalores \(\ell\):

\[ \Psi_{\rm D}(x) = \int_{-\infty}^{+\infty} b_{\rm D}(\ell) \delta(x-\ell) \mathrm{d}\ell._{} \tag{4.38} \]

Temos que \(\widehat x\) forma uma base contínua de autoestados. Foi mencionado na mesma [ seção 4.3 ], que para uma base contínua, o coeficiente da superposição pode ser assim determinado:

\[ b_{\rm D}(\ell) = \int_{-\infty}^{+\infty} \delta(x-\ell) \Psi_{\rm D}(x)\mathrm{d}x._{} \tag{4.39} \]

Substituindo (4.36) em (4.39), temos:

\[ b_{\rm D}(\ell)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} \delta(x-\ell) \mathrm{e}^{\large igx} \mathrm{d}x. \tag{4.40} \]

A integral (4.40) pode ser facilmente resolvida pela técnica da filtragem-delta [ seção 4.4 ], se percebemos que \(F(x)=\mathrm{e}^{\large igx}\):

\[ b_{\rm D}(\ell)= \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large ig\ell}_{}. \tag{4.41} \]

Para qualquer \(\ell\), \(-\infty < \ell < +\infty\), a densidade de probabilidade gerada por (4.41) é constante:

\[ |b_{\rm D}(\ell)|^2= \frac{1}{2\pi}._{} \tag{4.42} \]

Isso significa que a chance da partícula \({\rm D}\) ser encontrada com autovalor \(\ell_1\) é igual à chance de ser encontrada com autovalor \(\ell_2\), e assim por diante.

Em (4.38), a partícula \({\rm D}\) foi colocada na base do operador \(\widehat x\). E se ela fosse colocada na base operador \(\widehat p\)? Os autoestados de \(\widehat p\) foram deduzidos na [ seção 4.5 ], com eles podemos escrever a superposição:

\[ \Psi_{\rm D}(x)=\int_{-\infty}^{+\infty} b_{\rm D}(k) \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large ikx} \mathrm{d}k._{} \tag{4.43} \]

A base \(\widehat p\) também é contínua, logo:

\[ b_{\rm D}(k)=\int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large -ikx} \Psi_{\rm D}(x) \mathrm{d}x._{} \tag{4.44} \]

Substituindo (4.36) em (4.44):

\[ b_{\rm D}(k) = \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large -ikx} \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large igx} \mathrm{d}x . \tag{4.45} \]

Vamos deixar (4.45) com aparência de delta de Dirac:

\[ b_{\rm D}(k)= \frac{1}{2\pi} \int_{-\infty}^{+\infty} \mathrm{e}^{\large -i(k-g)x} \mathrm{d}x. \tag{4.46} \]

Não há dúvida que (4.46) é a delta de Dirac na forma exponencial [ seção 4.4 ], assim:

\[ b_{\rm D}(k)= \delta(k-g). \tag{4.47} \]

Então, no espaço do momento, há dois resultados possíveis para a densidade de probabilidade:

\[ \begin{aligned} |b_{\rm D}(k)|^2 &= \infty, \,\,\, & {\rm se} \,\,\, k = g_{} ,\\ &= 0, \,\,\, & {\rm se} \,\,\, k \neq g . \end{aligned} \tag{4.48} \]

Como se vê, as chances da partícula \({\rm D}\) ser encontrada com momento \(k \neq g\) são nulas. Como era de se esperar, esta partícula \({\rm D}\) possui um único momento, \(k=g\).

As Figs. 4.2 e 4.3 apresentam as densidades de probabilidade do momento e da posição, respectivamente, os gráficos das equações (4.48) e (4.37), para a partícula partícula \({\rm D}\) preparada com momento \(\hbar k=50\) \(\left( \mathrm{Js\cdot m^{-1}} \right)\). Essas figuras reforçam a conclusão da [ seção 4.5 ]: a partícula \({\rm D}\) possui momento certo e posição totalmente incerta.

Nota: para facilitar a visualização, fixamos \(\hbar =1\) \(\left( \mathrm{Js} \right)\).

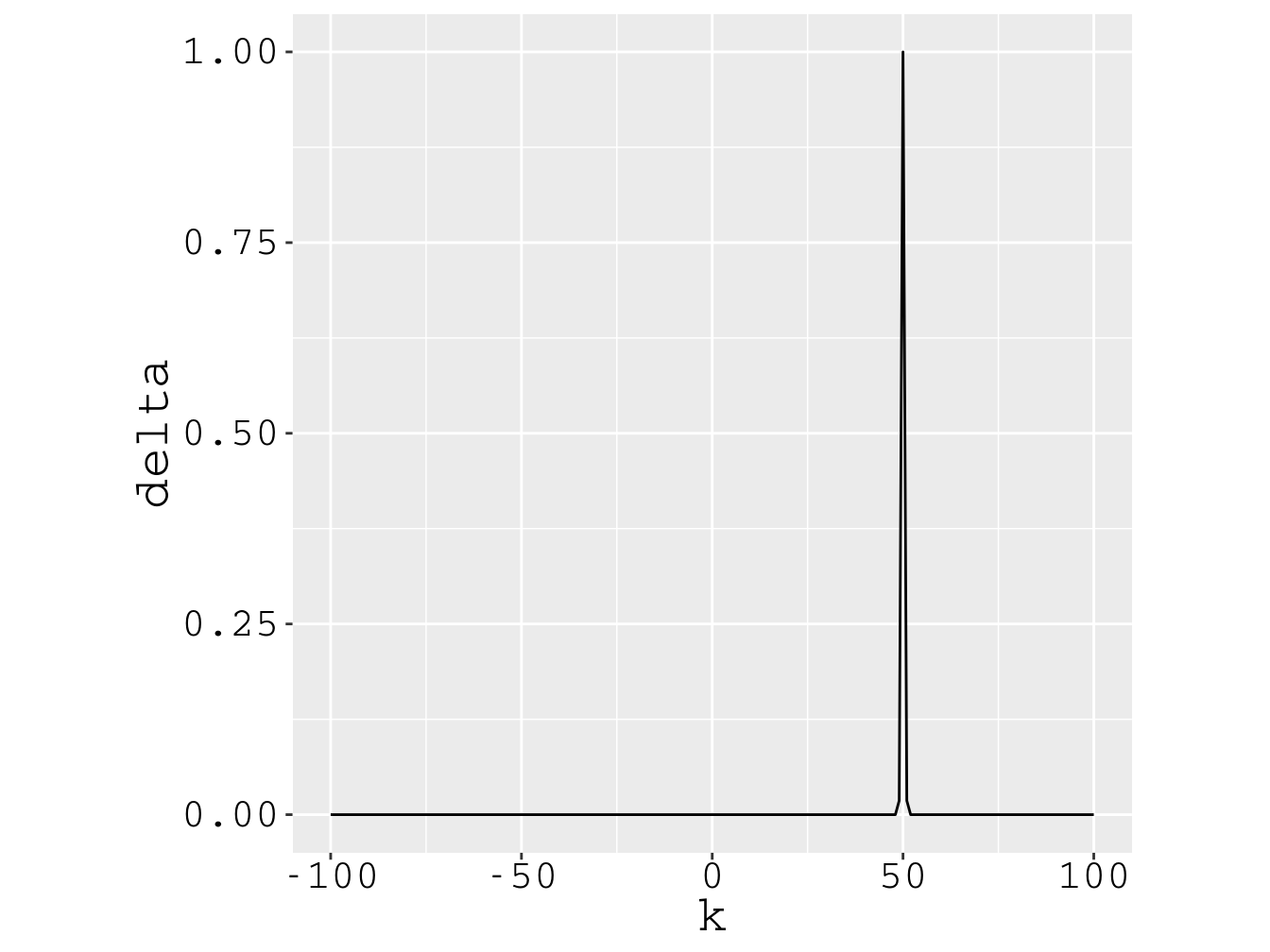
Figura 4.2: Partícula \({\rm D}\) com momento \(k=50\). A densidade de probabilidade do momento é delta de Dirac.

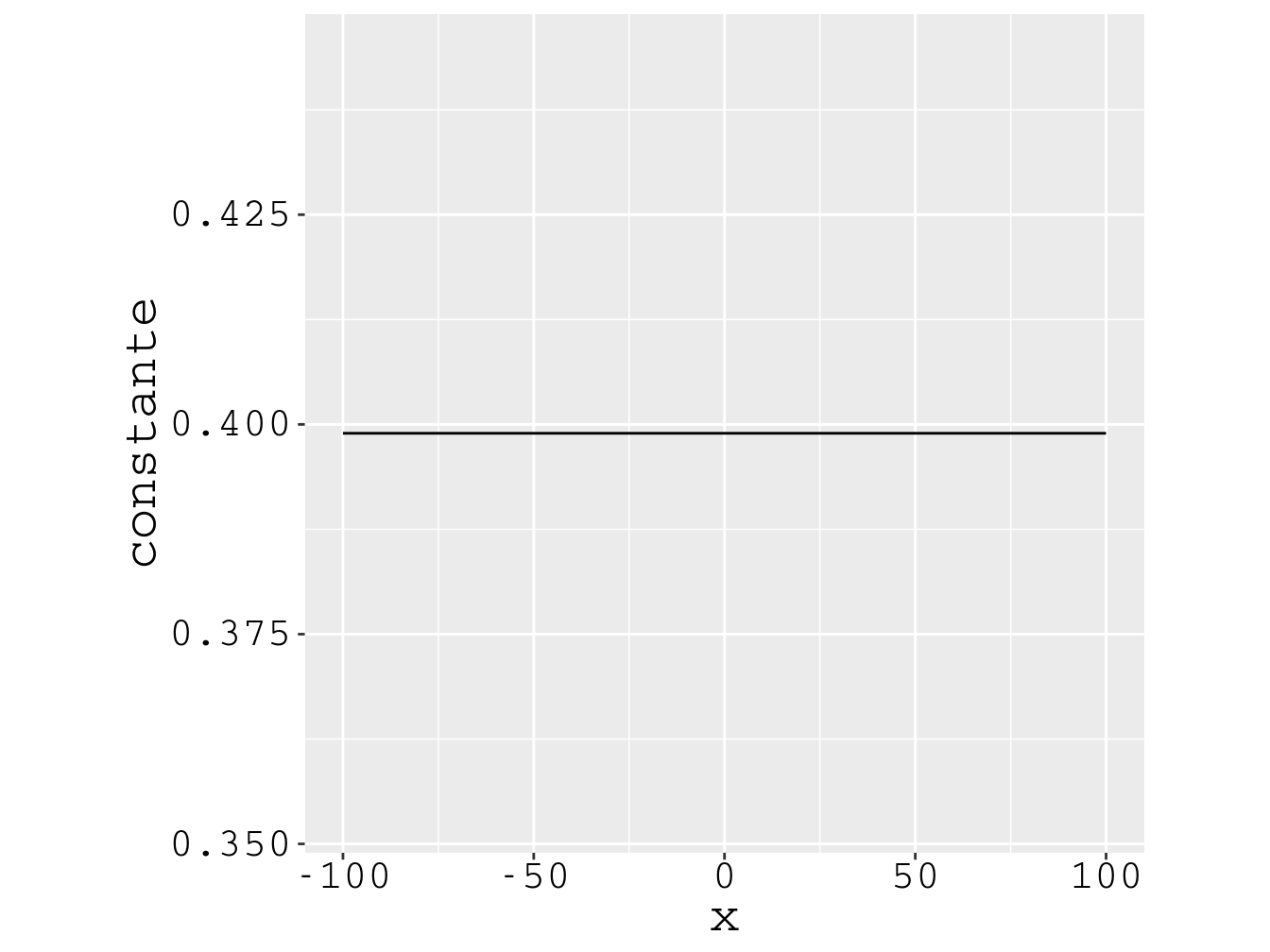
Figura 4.3: A mesma partícula \({\rm D}\), com momento \(k=50\). A densidade de probabilidade da posição é constante.

4.8 Mais sobre a partícula totalmente localizada

Chegou a hora de falarmos mais um pouco sobre a partícula totalmente localizada, batizada na [ seção 4.6 ] de partícula \({\rm L}\). Por ser delta de Dirac, entendemos que sua densidade de probabilidade também tem características de \(\delta\)-Dirac:

\[ \begin{aligned} \Psi_{\rm L}(x) &= \delta(x-\ell) .\\ |\Psi_{\rm L}(x)|^2 &= \infty, \,\,\, & {\rm se} \,\,\, x = \ell_{} ,\\ &= 0, \,\,\, & {\rm se} \,\,\, x \neq \ell . \end{aligned} \tag{4.49} \]

Apesar de sua posição ser certa, seu momento é totalmente incerto. Isso significa que a partícula \({\rm L}\) está numa superposição de autoestados de \(\widehat p\), conforme a expressão:

\[ \Psi _ {\rm L}(x)=\int_{-\infty}^{+\infty} b_{\rm L}(k) \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large ikx} \mathrm{d}k . \tag{4.50} \]

Onde o coeficiente da superposição é determinado por:

\[ \begin{aligned} b _ {\rm L}(k) &= \int _ {-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large -ikx} \Psi _ {\rm L}(x) \mathrm{d}x ;\\ &= \frac{1}{\sqrt{2\pi}} \int _ {-\infty}^{+\infty} \mathrm{e}^{\large -ikx} \delta(x-\ell) \mathrm{d}x . \end{aligned} \tag{4.51} \]

A integral (4.51) pode ser facilmente resolvida pela técnica da filtragem-delta [ seção 4.4 ], se percebemos que \(F(x)=\mathrm{e}^{\large -ikx}\):

\[ b _ {\rm L}(k) = \frac{1}{\sqrt{2\pi}} \mathrm{e}^{\large -ik\ell} . \tag{4.52} \]

Para qualquer \(k\), \(-\infty < k < +\infty\), a densidade de probabilidade gerada por (4.52) é constante:

\[ |b _ {\rm L}(k)|^2 = \frac{1}{2\pi} . \tag{4.53} \]

Isso significa que a chance da partícula \({\rm L}\) ser encontrada com momento \(k_1\) é igual à chance de se encontrada com momento \(k_2\), e assim por diante.

As Figs. 4.4 e 4.5 apresentam as densidades de probabilidade da posição e do momento, respectivamente, os gráficos das equações (4.49) e (4.53), para a partícula partícula \({\rm L}\) preparada na posição \(x=50\) \(\left( \mathrm{m} \right)\). Já essas figuras reforçam a conclusão da [ seção 4.6 ]: a partícula \({\rm L}\) possui posição certa e momento totalmente incerto.

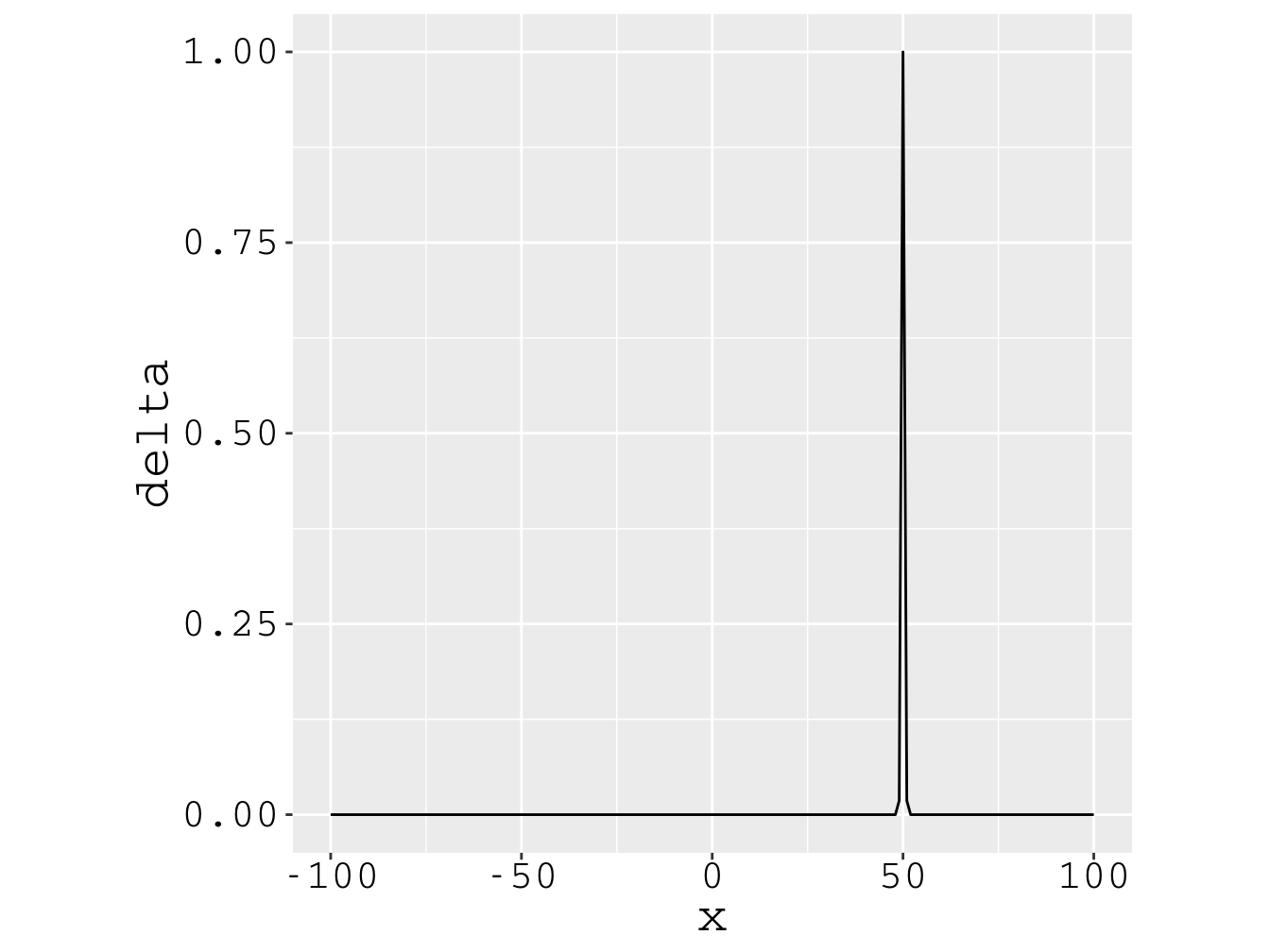
Figura 4.4: Partícula \({\rm D}\) na posição \(x=50\). A densidade de probabilidade da posição é delta de Dirac.

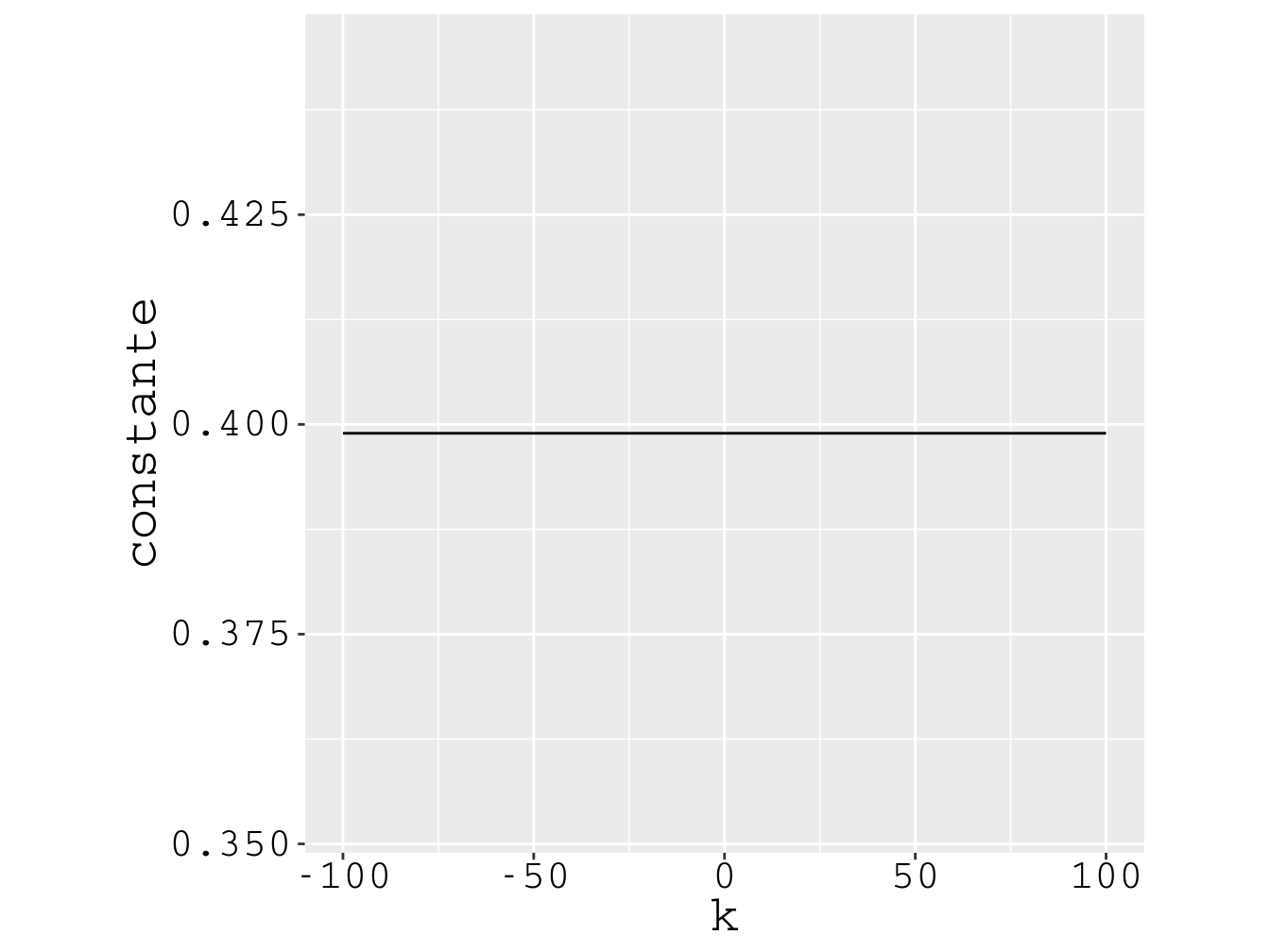
Figura 4.5: A mesma partícula \({\rm D}\), na posição \(x=50\). A densidade de probabilidade do momento é constante.