Capítulo 3 A DISTRIBUIÇÃO DE PROBABILIDADE QUÂNTICA

3.1 Introdução

Dentro da interpretação probabilística da mecânica quântica, desenvolvida por Max Born (1926), vamos nos deparar com métodos estatísticos, por exemplo, a determinação do resultado médio, do desvio padrão, de uma distribuição de resultados. É proveitoso, então, revermos alguns conceitos de estatística para, logo em seguida, podermos trabalhar com a probabilidade quântica.

3.2 A distribuição de probabilidade discreta

A observação de um fenômeno natural permite aumentar o conhecimento das leis que regem esse fenômeno. A compreensão será mais apurada se realizarmos uma série de testes sob as mesmas condições, digamos, com \(N\) repetições.

Os resultados dos testes serão designados por \(R_j\), \(j=1,2,3...,\eta\), e a ocorrência desses resultados por \(O(R_j)\). Por exemplo, num procedimento experimental com 100 repetições, \(N=100\), podemos encontrar o resultado \(R_1=7\), com ocorrência \(O(R_1)=50\). Dizemos, então, que a probabilidade desse resultado é igual a 50/100, ou seja, \(P(R_1)=0,50\). Generalizando, a probabilidade do resultado \(R_j\) é:

\[ P(R_j)= \frac{O(R_j)}{N}. \tag{3.1} \]

Tendo calculado a probabilidade de cada resultado, temos em mãos a distribuição de probabilidade do nosso experimento, então, podemos determinar o resultado médio dos testes \(\langle R \rangle\), através da somatória:

\[ \langle R \rangle = \sum_{j=1}^{\eta} P(R_j) R_j. \tag{3.2} \]

Por exemplo, num experimento com \(N=100\) testes e \(\eta=2\) resultados, \(R_1=2\) e \(R_2=10\), tendo ocorrências \(O(2)=20\) e \(O(10)=80\), temos a distribuição de probabilidade \(P(2)=0,\!20\) e \(P(10)=0,\!80\), com média \(\langle R \rangle = 0,\!20 \cdot 2 + 0,\!80 \cdot 10 = 8,\!4\).

Note que, nesse caso, a média não coincidiu com os resultados dos testes. Esse comentário é relevante, pois, em mecânica quântica, a média é chamada de valor esperado, passando a ideia de que o valor esperado vai estar na lista dos resultados. Como vimos, o valor esperado (média) é um dado estatístico que caracteriza a distribuição dos resultados. Naturalmente, há ocasiões em que o valor esperado vai coincidir com um dos resultados do experimento. Também, não devemos confundir valor esperado (média) com valor mais provável, isto é, aquele resultado que possui maior probabilidade de ocorrer, no nosso exemplo, \(P(10)=0,\!80\), o que nos leva a concluir que o valor mais provável é \(R_2=10\).

A distribuição de probabilidade também é caracterizada pelo desvio padrão \(\sigma\) dos resultados dos testes ao redor da média:

\[ \sigma = \sqrt{ \langle R^2 \rangle - \langle R \rangle ^2 }. \tag{3.3} \]

Essa notação pode embaralhar a visão, mas note a distinção entre cada um dos termos acima, principalmente o lugar do elevado ao quadrado; as fórmulas dos termos são bem diferentes:

\[ \langle R \rangle ^2 = \left( \sum_{j=1}^{\eta} P(R_j) R_j \right) ^2. \tag{3.4} \]

\[ \langle R^2 \rangle = \sum_{j=1}^{\eta} P(R_j) R_j^2. \tag{3.5} \]

Aplicando as equações (3.4) e (3.5) ao nosso exemplo, temos:

\[ \langle R \rangle ^2 = \left( 0,\!20 \cdot 2 + 0,\!80 \cdot 10 \right) ^2 = 70,\!56. \tag{3.6} \]

\[ \langle R^2 \rangle = 0,\!20 \cdot 2^2 + 0,\!80 \cdot 10^2 = 80,\!80. \tag{3.7} \]

O que implica em:

\[ \sigma = \sqrt{ 80,\!80 - 70,\!56 } = 3,\!2. \tag{3.8} \]

Portanto, a distribuição de probabilidade \(P(2)=0,\!20\) e \(P(10)=0,\!80\) é caracterizada pela média \(\langle R \rangle=8,4\) e desvio padrão \(\sigma = 3,\!2\), possuindo histograma como aparece na Fig. 3.1.

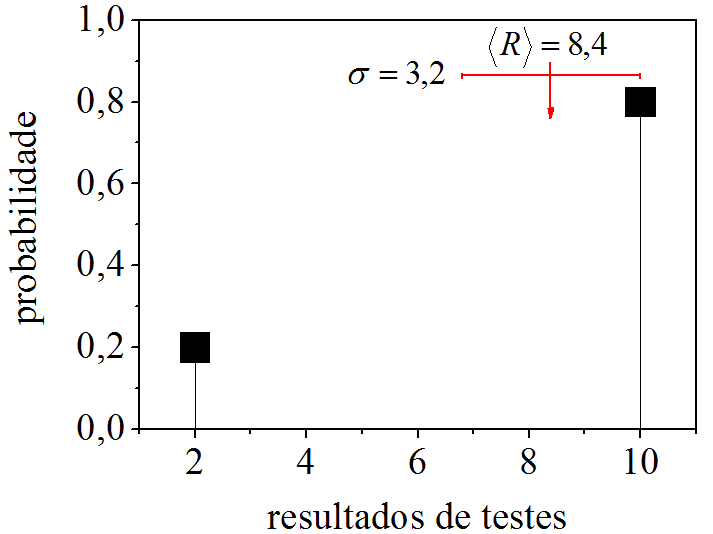
Figura 3.1: Histograma da distribuição de probabilidade \(P(2)=0,\!20\) e \(P(10)=0,\!80\).

Parece estranho a média cair no “vazio” dos resultados, mas como comentamos, ela é um dado estatístico. Para satisfazer nosso desejo de ver a média em cima de um dos resultados, foram preparadas duas distribuições cujos histogramas são apresentados na Fig. 3.2.

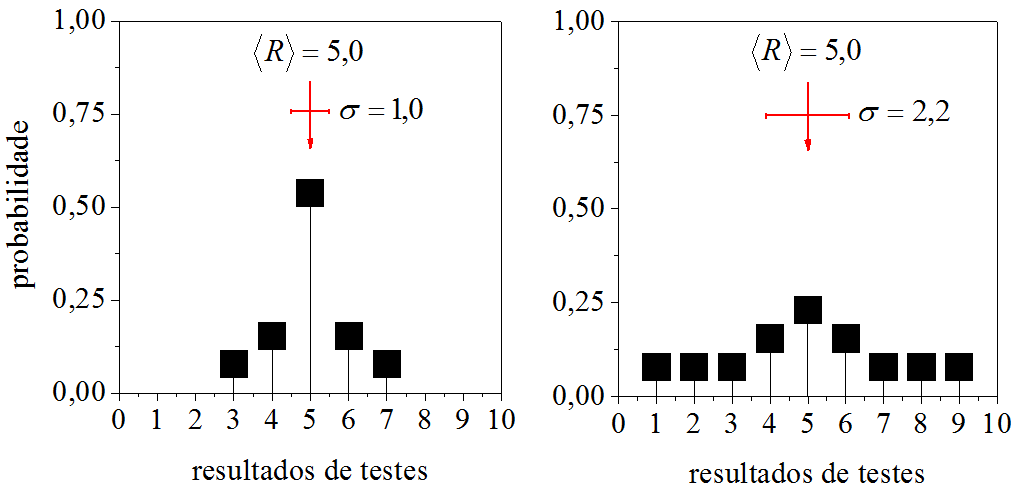
Figura 3.2: Histogramas onde a média coincide com um dos resultados.

Na Fig. 3.2, as duas distribuições possuem média \(\langle R \rangle=5,\!0\) a qual coincide com o resultado \(5,\!0\). A diferença está nos desvios padrões. Como se vê, o menor desvio, \(\sigma = 1,\!0\), veio da distribuição estreita e aguda, por outro lado, o maior desvio, \(\sigma = 2,\!2\) procede da distribuição larga e rasa. Esses histogramas nos ajudam a endender a ligação do desvio padrão com a dispersão dos resultados ao redor do resultado médio.

3.3 A distribuição de probabilidade contínua

Até o momento, descrevemos o tratamento estatístico de resultados discretos \(R_j\), mas também há resultados que fazem parte de um contínuo de números reais, \(u\). Estes obedecem, correspondentemente, a uma distribuição de probabilidade contínua, \(\rho(u)\).

A distribuição contínua não será uma distribuição de probabilidade genuína, significará uma densidade de probabilidade, ou probabilidade por intervalo unitário de \(u\). Em outras palavras, \(\rho(u)\) terá a dimensão do inverso da dimensão de \(u\). A probabilidade genuína será \(\rho(u)\mathrm{d}u\), interpretada como a probabilidade de um resultado de um experimento estar entre \(u\) e \(u+\mathrm{d}u\). Desse modo, a integral (3.9) determina a probabilidade de um resultado \(u\) estar no intervalo \(u_1 < u < u_2\), ou seja, a probabilidade genuína é a área sob a curva de \(\rho(u)\mathrm{d}u\).

\[ {\rm Pr}( u_1 < u < u_2 ) = \int_{u_1}^{u_2} \rho(u)\mathrm{d}u. \tag{3.9} \]

Fica fácil de entender que:

\[ \int_{-\infty}^{+\infty} \rho(u)\mathrm{d}u = 1_{}. \tag{3.10} \]

As definições de resultado médio de \(u\) e resultado médio de \(u^2\), vistas na [ seção 3.2 ], agora são generalizadas para o caso contínuo:

\[ \langle u \rangle = \int_{-\infty}^{+\infty} u \rho(u)\mathrm{d}u._{} \tag{3.11} \]

\[ \langle u^2 \rangle = \int_{-\infty}^{+\infty} u^2 \rho(u)\mathrm{d}u._{} \tag{3.12} \]

A fórmula para calcular o desvio padrão não muda:

\[ \sigma_u = \sqrt{ \langle u^2 \rangle - \langle u \rangle ^2 }. \tag{3.13} \]

Como exemplo de distribuição de probabilidade contínua, podemos citar a distribuição gaussiana:

\[ G(u)=\frac{1}{\sqrt{2\pi }} \frac{1}{\sigma_u} \mathrm{exp} \left(-\frac{(u-\langle u \rangle )^2}{2\sigma_u^2} \right). \tag{3.14} \]

A Fig. 3.3 apresenta duas gaussianas que diferem no valor do desvio padrão, \(\sigma_u=5\) e \(\sigma_u=10\), mas possuem a mesma média, \(\langle u \rangle=50\).

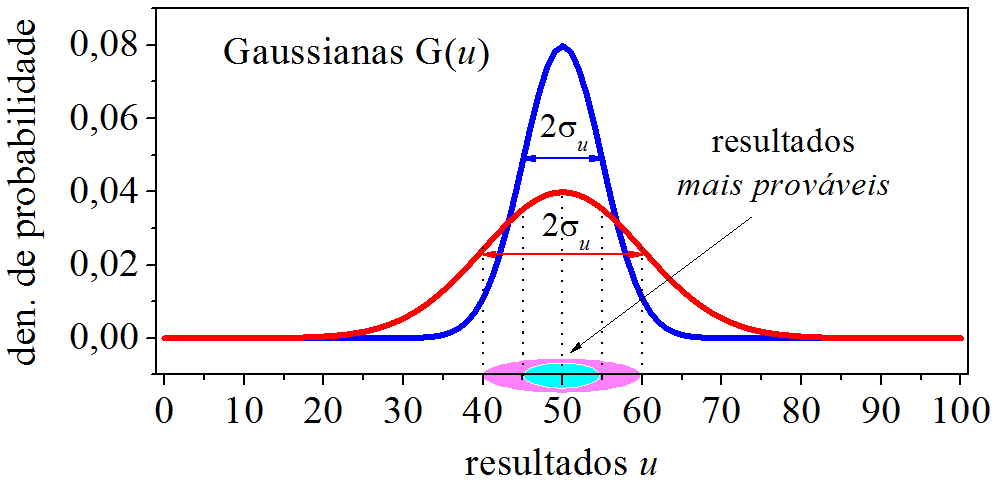
Figura 3.3: Gaussianas.

Analisando as gaussianas, os resultados que se alojam na faixa \(2\sigma_u\), ao redor da média, farão parte significativa das medições. Dizemos que estes resultados são mais prováves de ocorrerem. Na gaussiana estreita, os resultados mais prováveis estão entre \(45<u<55\), na larga, entre \(40<u<60\).

3.4 A distribuição de probabilidade quântica

Quais foram os destaques do [ capítulo 1 ], [ seções 1.2 e 1.3 ]? Lá fomos apresentados à função de onda independente do tempo \(\psi(x)\) e interpretamos \(|\psi(x)|^2\). O que foi mesmo que Max Born postulou? Ele postulou que o módulo ao quadrado da função de onda significa densidade de probabilidade. Então, com o conhecimento adquirido na [ seção 3.3 ], podemos escrever:

\[ \rho(x) = |\psi(x)|^2 = \psi^{\ast}(x)\psi(x). \tag{3.15} \]

Se resolvermos a equação de Schrödinger de uma partícula \(m\) sob influência de um potencial \(V(x)\), descobriremos sua função de onda e sua densidade de probabilidade. Daí, se formos investigar a posição dessa partícula, teremos a probabilidade \(|\psi(x)|^2\mathrm{d}x\) de encontrá-la entre \(x\) e \(x+\mathrm{d}x\). Também estaremos aptos para calcular a probabilidade de encontrá-la entre \(x_1\) e \(x_2\), fazendo:

\[ {\rm Pr}( x_1 < x < x_2 ) = \int_{x_1}^{x_2} |\psi(x)|^2 \mathrm{d}x. \tag{3.16} \]

Ademais, poderemos determinar o resultado médio e o resultado médio, ao quadrado, de sua posição:

\[ \langle x \rangle = \int_{-\infty}^{+\infty} x |\psi(x)|^2\ \mathrm{d}x._{} \tag{3.17} \]

\[ \langle x^2 \rangle = \int_{-\infty}^{+\infty} x^2 |\psi(x)|^2\ \mathrm{d}x._{} \tag{3.18} \]

Por fim, poderemos saber o valor do desvio padrão de sua posição:

\[ \sigma_x = \sqrt{ \langle x^2 \rangle - \langle x \rangle ^2 }. \tag{3.19} \]

O desvio padrão é reflexo da dispersão da presença da partícula no espaço. Mas podemos pensar mais além. Aqui vamos interpretar estatisticamente a incerteza da posição, dizendo:

– A incerteza da posição é o próprio desvio padrão, \(\Delta x = \sigma_x\).

Esse vínculo faz sentido. O desvio padrão está relacionado à dispersão das prováveis posições da partícula sujeita a certo potencial \(V(x)\), então, o valor do desvio está diretamente ligado à indeterminação da posição dessa partícula no espaço. Temos, assim, um procedimento estatístico para determinar a incerteza da posição, que consiste em usar a mesma fórmula do cálculo do desvio padrão da posição:

\[ \Delta x = \sqrt{ \langle x^2 \rangle - \langle x \rangle ^2 }. \tag{3.20} \]

A mesma interpretação estatística se aplica à indeterminação envolvendo o momento dessa partícula: \(\Delta p = \sigma_p\).

Como calcular \(\sigma_p\)? Poderíamos partir do principio de incerteza, pois sabendo o valor de \(\sigma_x\), este princípio poderia nos auxilia a estimar o valor do desvio padrão do momento: \(\sigma_x \sigma_p \geqslant \hbar/2\). Mas só estimar não basta. Precisamos do procedimento estatístico. Então, (a) como determinar \(\sigma_p\)? Não há dúvida que a metodologia estatística é semelhante ao que escrevemos na equação (3.19), sendo assim, podemos escrever para o desvio padrão do momento:

\[ \sigma_p = \sqrt{ \langle p^2 \rangle - \langle p \rangle ^2 }. \tag{3.21} \]

Bem, agora a questão passa a ser: (b) como determinar as médias que aparecem na equação (3.21)? Sem dúvida, adaptando as fórmulas (3.17) e (3.18):

\[ \langle p \rangle = \int_{-\infty}^{+\infty} p |\psi(p)|^2\ \mathrm{d}p._{} \tag{3.22} \]

\[ \langle p^2 \rangle = \int_{-\infty}^{+\infty} p^2 |\psi(p)|^2\ \mathrm{d}p._{} \tag{3.23} \]

Chegamos, então, à pergunta: (c) como determinar a densidade de probabilidade do momento \(|\psi(p)|^2\)? Fazendo analogia com a equação (3.15):

\[ |\psi(p)|^2 = \psi^{\ast}(p)\psi(p). \tag{3.24} \]

Por fim, nos deparamos com a questão fundamental: (d) como determinar a função de onda no espaço do momento, \(\psi(p)\)? Há duas maneiras de encarar essa questão. Podemos determinar a transformada de Fourier da equação de Schrödinger da posição e, assim, trabalhar diretamente no espaço do momento. As passagens matemáticas serão omitidas, mas a equação diferencial a ser resolvida é esta:

\[ \frac{p^2}{2m}\psi(p) + i\hbar \frac{\partial \psi(p)}{\partial p} V(p) = E\psi(p). \tag{3.25} \]

Resolvendo (3.25), encontraremos \(\psi(p)\). A outra maneira é resolver a equação de Schrödinger no espaço da posição [ seção 1.3 ], deteminar a função de onda da posição e, em seguida, determinar a transformada de Fourier da própria \(\psi(x)\), encontrando a função de onda do momento sem a necessidade de se resolver a equação diferencial (3.25):

\[ \psi(p)= \frac{1}{\sqrt{2\pi\hbar}} \int_{-\infty}^{+\infty} \psi(x) \mathrm{e}^{\large \frac{-ipx}{\hbar}} \mathrm{d}x._{} \tag{3.26} \]

3.5 A distribuição de probabilidade periódica

Há situações em que os resultados dos testes vão se acomodar de maneira repetitiva. A Fig. 3.4 mostra densidades de probabilidade que são periódicas. Vemos que \(|\psi _2(x)|^2\), \(|\psi _3(x)|^2\), \(|\psi _4(x)|^2\) e \(|\psi _5(x)|^2\) apresentam posições mais prováveis (ao redor dos máximos das curvas), menos prováveis (ao redor dos mínimos) e até improváveis (nos zeros), que se repetem ao longo do eixo \(x\). Vemos também que o número de máximos (picos) aumenta de maneira gradual, porém, todas as densidades apresentam a mesma média \(\langle x \rangle=a/2\). Nas densidades pares a média “cai no vazio” dos resultados, enquanto que nas ímpares coincide com o valor \(x=a/2\).

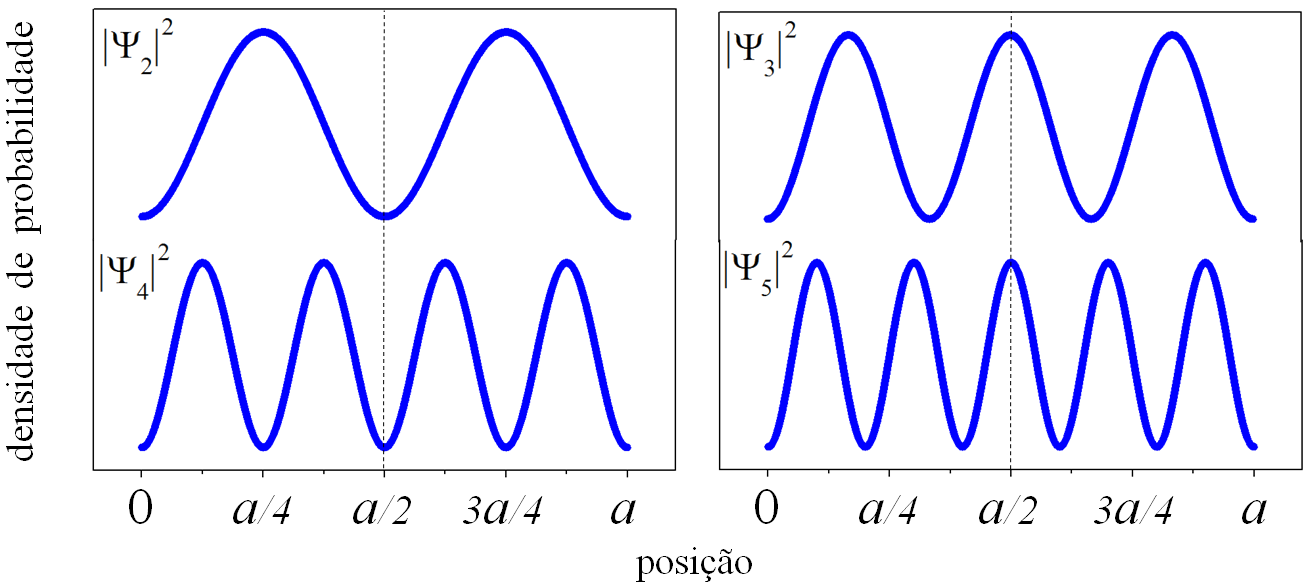
Figura 3.4: Densidades de probabilidade periódicas.

Se o desvio padrão de uma distribuição gaussiana [ seção 3.3 ] pode ser localizado ao redor do pico da gaussiana, então, quando trabalharmos com a distribuição periódica \(|\psi _n(x)|^2\) (que possui \(n\) picos), podemos pensar em dividir \(\sigma _n\) por \(n\). Geometricamente, podemos pensar em distribuir a quantidade \(\sigma _n /n\) ao redor de cada máximo dessa distribuição. Para ilustrar, a Fig. 3.5 mostra como fica o desvio padrão \(\sigma _2\) distribuído pelos máximos da densidade de probabilidade periódica \(|\psi _2(x)|^2\).

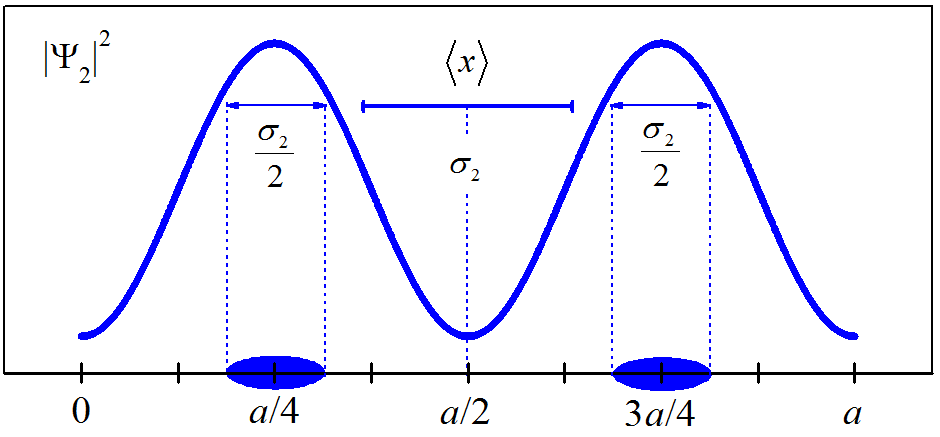
Figura 3.5: Ilustração do desvio padrão distribuído ao redor de máximos.