Capítulo 8 A BARREIRA RETANGULAR

8.1 Introdução

A barreira retangular de potencial é caracterizada por ser descontinua em 2 pontos do espaço. Escolhemos a descontinuidade na origem e em \(x=a\):

\[ \begin{aligned} V(x) &= 0, & {\rm se\ \ } & x < 0 ,\\ &= V_0, & {\rm se\ \ } & 0 \leqslant x \leqslant a ,\\ &= 0, & {\rm se\ \ } & x > a . \end{aligned} \tag{8.1} \]

Aqui, \(V_0\) é uma grandeza positiva. Visualizamos a barreira retangular na Fig. 8.1.

Figura 8.1: A barreira retangular de potencial.

Comparando com o degrau, que se se estende por todo semi-eixo positivo [ seção 7.1 ], a barreira atua somente em certa região do espaço. Os efeitos quânticos por ela manifestados, dependem da energia da partícula incidente. Na [ seção 8.2 ], estudaremos o caso da energia da partícula ser menor que a altura da bareira. Já na [ seção 8.3 ], trataremos o caso de \(E\) ser maior que \(V_0\).

8.2 O regime de baixa energia

O regime de baixa energia é caracterizado por \(E < V_0\). A barreira divide o espaço em três regiões. Há a região de dentro (\({\rm D}\)) e as regiões de fora (\({\rm F}\)) da barreira. Em cada região, a solução da equação de Schrödinger apresenta uma peculiar expressão:

\[ \begin{aligned} \psi_{\rm F} &= A\, \mathrm{e}^{\large ikx} + B\, \mathrm{e}^{\large -ikx}, & x < 0 ,\\ \psi_{\rm D} &= C\, \mathrm{e}^{\large ik_{\rm D}x} + D\, \mathrm{e}^{\large -ik_{\rm D}x}, & 0 \leqslant x \leqslant a ,\\ \psi_{\rm F} &= F\, \mathrm{e}^{\large ikx} + G\, \mathrm{e}^{\large -ikx}, & x > a . \end{aligned} \tag{8.2} \]

Em cada região, o número de onda também apresenta uma peculiar expressão:

\[ \begin{aligned} k &= \frac{\sqrt{2mE}}{\hbar}, & x < 0 ,\\ k_{\rm D} &= \frac{\sqrt{2m(E - V_0)}}{\hbar}, & 0 \leqslant x \leqslant a ,\\ k &= \frac{\sqrt{2mE}}{\hbar}, & x > a . \end{aligned} \tag{8.3} \]

Por causa de \(E<V_0\), o número de onda dentro da barreira é imaginário. É favorável escrevê-lo na forma: \(k_{\rm D}=iq\), onde \(q\) é um número real e positivo:

\[ q = \frac{\sqrt{2m(V_0 - E)}}{\hbar}. \tag{8.4} \]

Após a transmissão através da barreira, não há motivos para a onda ser refletida, então podemos ajustar \(G=0\). Ademais, substituindo (8.4) em (8.2), a solução da barreira retangular se escreve:

\[ \begin{aligned} \psi_{\rm F} &= A\, \mathrm{e}^{\large ikx} + B\, \mathrm{e}^{\large -ikx}, & x < 0 ,\\ \psi_{\rm D} &= C\, \mathrm{e}^{\large -qx} + D\, \mathrm{e}^{\large qx}, & 0 \leqslant x \leqslant a ,\\ \psi_{\rm F} &= F\, \mathrm{e}^{\large ikx}, & x > a . \end{aligned} \tag{8.5} \]

Explorando (8.5), a onda de matéria incidente \(A\) pode aparecer do outro lado da barreira, na forma da onda transmitida \(F\), ou aparecer na frente da barreira, na forma da onda refletida \(B\). Já dentro da barreira, ocorre certa “competição” entre as exponenciais reais \(C\) e \(D\).

O módulo de \(A\), ao quadrado, é a probabilidade por unidade de comprimento que a partícula incidente “carrega” em direção à barreira. Analogamente, o módulo de \(F\), ao quadrado, é a probabilidade que a partícula transmitida “carrega” em direção ao infinito. Por causa da barreira, que dificulta a transmissão de probabilidades, \(|F|^2\) nunca será maior que \(|A|^2\). O valor máximo que se pode atingir é \(|F|^2 = |A|^2\). Então, para analisarmos a transmissão por uma barreira é útil estudarmos o comportamento da razão:

\[ T = \frac{ |F|^2 }{ |A|^2 }. \tag{8.6} \]

A razão (8.6) é adimensional e exprime a probabilidade de transmissão da partícula através da barreira. Ela é chamada de coeficiente de transmissão. Nosso trabalho agora será encontrar a expressão desse coeficiente. Podemos começar reescrevendo (8.6) na forma:

\[ \frac{1}{T} = \frac{ A^{\ast}A }{ F^{\ast}F }. \tag{8.7} \]

Segundo (8.7), nossa busca se resume em encontrar a expressão de \(A/F\). Para isso, podemos estabelecer as ligações entre as constantes complexas, \(A\), \(B\), \(C\), \(D\), e \(F\), por se valer das condições de continuidade da função de onda nas interfaces da barreira:

\[ \newcommand{ \FF }{ _ {\rm F} } \newcommand{ \DD }{ _ {\rm D} } {\rm Interface}\ x=0\ \left\{ \begin{array}{l} \psi\FF(0) = \psi\DD(0) \\ \dfrac{\mathrm{d} \psi\FF(0)}{\mathrm{d}x} = \dfrac{\mathrm{d} \psi\DD(0)}{\mathrm{d}x} \end{array} \right. \tag{8.8} \]

\[ {\rm Interface}\ x=a\ \left\{ \begin{array}{l} \psi\DD(a) = \psi\FF(a) \\ \dfrac{\mathrm{d} \psi\DD(a)}{\mathrm{d}x} = \dfrac{\mathrm{d} \psi\FF(a)}{\mathrm{d}x} \end{array} \right. \tag{8.9} \]

Resolvendo (8.8) e (8.9), encontramos:

\[ {\rm Interface}\ x=0\ \left\{ \begin{array}{l} A + B = C + D \\ ikA - ikB = -qC + qD \end{array} \right. \tag{8.10} \]

\[ {\rm Interface}\ x=a\ \left\{ \begin{array}{l} C\,\mathrm{e}^{\large -qa} + D\,\mathrm{e}^{\large qa} = F\,\mathrm{e}^{\large ika} \\ -q C\,\mathrm{e}^{\large -qa} + q D\,\mathrm{e}^{\large qa} = ik F\, \mathrm{e}^{\large ika} \end{array} \right. \tag{8.11} \]

Vamos trabalhar (8.11) duas vezes:

\(1^{a}.\) Ao subtrair as equações, encontramos \(C\) em função de \(F\):

\[ C = \frac{q -ik}{2q} \, \mathrm{e}^{\large qa} F\, \mathrm{e}^{\large ika} . \tag{8.12} \]

\(2^{a}.\) Ao somar as equações, encontramos \(D\) em função de \(F\):

\[ D = \frac{q +ik}{2q} \, \mathrm{e}^{\large -qa} F\, \mathrm{e}^{\large ika} . \tag{8.13} \]

Agora, eliminando o \(B\) das equações (8.10), encontramos uma relação muito útil, que vai nos auxiliar a atingir nosso objetivo:

\[ 2ikA = D(q + ik) -C(q - ik). \tag{8.14} \]

Substituindo (8.12) e (8.13) em (8.14), encontramos:

\[ 2ikA = \frac{(q +ik)^2}{2q} \, \mathrm{e}^{\large -qa} F\, \mathrm{e}^{\large ika} - \frac{(q -ik)^2}{2q} \, \mathrm{e}^{\large qa} F\, \mathrm{e}^{\large ika}. \tag{8.15} \]

Pela primeira vez temos algo que relaciona A com F:

\[ \frac{A}{F} = \frac{(q+ik)^2}{4iqk}\, \mathrm{e}^{\large -qa} \, \mathrm{e}^{\large ika} - \frac{(q-ik)^2}{4iqk}\, \mathrm{e}^{\large qa} \, \mathrm{e}^{\large ika}. \tag{8.16} \]

Resolvendo os termos quadráticos de (8.16) e, em seguida, agrupando as exponenciais reais:

\[ \frac{A}{F} = \frac{1}{2}\, (\mathrm{e}^{\large qa} + \mathrm{e}^{\large -qa}) \, \mathrm{e}^{\large ika} - \frac{(q^2 - k^2)}{4iqk}\, (\mathrm{e}^{\large qa} - \mathrm{e}^{\large -qa}) \, \mathrm{e}^{\large ika}. \tag{8.17} \]

Identificamos as relações trigonométricas:

\[ \begin{aligned} \mathrm{e}^{\large qa} +\mathrm{e}^{\large -qa} &=2{\rm cosh}(qa) ,\\ \mathrm{e}^{\large qa} -\mathrm{e}^{\large -qa} &=2{\rm senh}(qa) . \end{aligned} \tag{8.18} \]

Substituindo (8.18) em (8.17), temos a relação que procurávamos:

\[ \frac{A}{F} = {\rm cosh}(qa)\, \mathrm{e}^{\large ika} - \frac{(q^2 - k^2)}{2iqk}\, {\rm senh}(qa)\, \mathrm{e}^{\large ika}. \tag{8.19} \]

Para encontrar o coeficiente de transmissão, há necessidade de fazer o complexo conjugado de (8.19):

\[ \left( \frac{A}{F} \right)^{\ast} = {\rm cosh}(qa)\, \mathrm{e}^{\large -ika} + \frac{(q^2 - k^2)}{2iqk}\, {\rm senh}(qa)\, \mathrm{e}^{\large -ika}. \tag{8.20} \]

Enfim, podemos determinar (8.7) através das relações (8.19) e (8.20):

\[ \frac{1}{T} = {\rm cosh}^2(qa) + \frac{\left( q^2 - k^2 \right)^2}{4q^2k^2}\, {\rm senh}^2(qa). \tag{8.21} \]

Lembrando que \({\rm cosh}^2(qa) = 1 + {\rm senh}^2(qa)\):

\[ \frac{1}{T} = 1 + \left[ 1+ \frac{\left( q^2 - k^2 \right)^2}{4q^2k^2}\right] {\rm senh}^2(qa). \tag{8.22} \]

Resolvendo os colchetes, chegamos à expressão final do coeficiente de transmissão para o caso do regime de \({\rm b}\)aixa energia:

\[ \frac{1}{T_{\rm b}} = 1 + \frac{\left( k^2 + q^2 \right)^2}{4k^2q^2}\, {\rm senh}^2(qa)._{} \tag{8.23} \]

8.3 O regime de alta energia

O regime de alta energia é caracterizado por \(E > V_0\). Seguindo a nomenclatura da [ seção 8.2 ], a solução da equação de Schrödinger por toda extensão da barreira retangular é:

Em cada região, o número de onda também apresenta uma peculiar expressão:

Nosso objetivo aqui também é determinar o coeficiente de transmissão. Começamos aplicando as condições de continuidade das funções de onda nas interfaces da barreira:

\[ \newcommand{ \FF }{ _ {\rm F} } \newcommand{ \DD }{ _ {\rm D} } \newcommand{ \kD }{ k _ {\rm D} } {\rm Interface}\ x=0\ \left\{ \begin{array}{l} A + B = C + D \\ ikA - ikB = i\kD C - i\kD D \end{array} \right. \tag{8.26} \]

\[ {\rm Interface}\ x=a\ \left\{ \begin{array}{l} C\,\mathrm{e}^{\large i\kD a} + D\,\mathrm{e}^{\large -i\kD a} = F\,\mathrm{e}^{\large ika} \\ i\kD C\,\mathrm{e}^{\large i\kD a} -i\kD D\,\mathrm{e}^{\large -i\kD a} = ik F\, \mathrm{e}^{\large ika} \end{array} \right. \tag{8.27} \]

Ao compararmos as equações (8.26) e (8.27) com as correspondentes da [ seção 8.2 ], fica evidente que a única diferença entre elas é a permuta:

\[ q \iff -i\kD. \tag{8.28} \]

Assim, a única coisa a fazer é fazer a permuta (8.28) na expressão final do coeficiente de transmissão deduzido na [ seção 8.2 ]:

\[ \frac{1}{T_{\rm b}} = 1 + \frac{\left( k^2 + q^2 \right)^2}{4k^2q^2} \, {\rm senh}^2(qa), \tag{8.29} \]

\[ \frac{1}{T} = 1 + \frac{ \left( k^2 + [-ik_{\rm D}]^2 \right)^2 } { 4 k^2 [-ik_{\rm D}]^2 } \, {\rm senh}^2([-ik_{\rm D}]a). \tag{8.30} \]

Cabe a recordação:

\[ {\rm senh}^2(\pm ikx) = - {\rm sen}^2(kx). \tag{8.31} \]

Substituindo (8.31) em (8.30), chegamoas à expressão final do coeficiente de transmissão para o caso do regime de \({\rm a}\)lta energia:

\[ \frac{1}{T_{\rm a}} = 1+ \frac{ \left( k^2 - k_{\rm D}^2 \right)^2 } { 4k^2 k_{\rm D}^2 } \, {\rm sen}^2(k_{\rm D}a). \tag{8.32} \]

8.4 Um exemplo numérico

Estamos com as ferramentas preparadas para estudar a transmissão em barreiras de potencial. Analisaremos um elétron incidindo em uma barreira de altura \(V_0=200\ {\rm meV}\) e espessura \(a=20\ \unicode{xC5}\). Tomando como base a altura da barreira, dividimos a energia do elétron em dois intervalos: \(0 < E < V_0\) [ \(T_{\rm b}\), seção 8.2 ] e \(V_0 < E < 10V_0\) [ \(T_{\rm a}\), seção 8.3 ]. A Fig. 8.2 apresenta os gráficos dos coeficientes de transmissão \(T_{\rm b}\) e \(T_{\rm a}\).

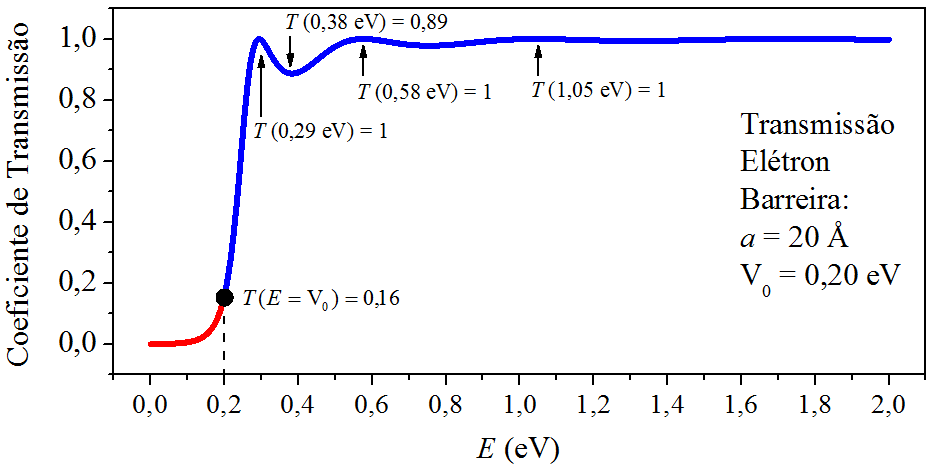
Figura 8.2: A transmissão por uma barreira retangular de potencial.

A Fig. 8.2 mostra alguns pontos em destaque. Existem energias especiais que proporcionam \(T_{\rm a}=1\), quer dizer, há 100% de chance da partícula ser transmitida através da barreira. A partícula “chega, e passa.” Isso ocorre nas energias \(E=290\ {\rm meV}\), \(E=580\ {\rm meV}\) e \(E=1050\ {\rm meV}\). Vendo por outro ângulo, quer dizer que não há chance da partíula sofrer reflexão nas interfaces da barreira. Investigando a expressão do coeficiente de transmissão no regime de alta energia, a condição para \(T_{\rm a} = 1\) é \({\rm sen}(k_{\rm D}a) = 0\), ou seja:

\[ k_{\rm D} = \frac{n\pi}{a}, \ \ \ \ \ n=1,2,3... \tag{8.33} \]

Dentro da barreira, o número de onda é [ seção 8.3 ]:

\[ k_{\rm D} = \frac{\sqrt{2m(E - V_0)}}{\hbar}. \tag{8.34} \]

Substituindo (8.33) em (8.34), encontramos a expressão das energias que geram 100% de transmissão:

\[ E_n = V_0 + \frac{n^2 \pi^2 \hbar^2}{2 m a^2}. \tag{8.35} \]

As energias que condicionam transmissão máxima são chamadas de energias de ressonância da barreira. Nossa dedução mostra que a energia de ressonância é quantizada. Além disso, mostra que o termo que quantiza a expressão é idêntico à energia de confinamento de um poço retangular infinito, de largura igual à largura da barreira [ver seção 6.2 ].

Observando mais um pouco a Fig. 8.2, percebemos que muitas energias geram \(T_{\rm a} < 1\). Por exemplo, \(E=380\ {\rm meV}\) gera \(T_{\rm a} = 0,\!89\). Se há \(89\%\) de chance da partícula ser transmitida através da barreira, também há \(11\%\) dela ser refletida! Isso viola a visão clássica sobre o problema, que afirma que uma partícula tendo energia maior que uma barreira não poderia ser refletida por ela. De fato, na mecânica quântica:

\[ T + R = 1. \tag{8.36} \]

Onde \(R\) é o coeficiente de reflexão.

A análise do regime de baixa energia, início da curva da Fig. 8.2, mostra que esse regime produz grande reflexão. Por exemplo, \(E=200\ {\rm meV}\) gera \(T_{\rm b} = 0,\!16\), o que implica em \(R_{\rm b} = 0,\!84\). Se compararmos as probabilidades, agora a partícula tem mais chance de ser refletida do que transmitida. Mas ainda existe certa chance, mesmo que pequena, da partícula ser transmitida! Esse fato puramente quântico também abala a visão clássica do problema, que afirma que uma partícula com energia menor que uma barreira não poderia transpor esse potencial.

8.5 O tunelamento

A transmissão quântica por barreiras, quando a energia da partícula é menor que a energia potencial da barreira, é chamada de tunelamento. Dentro da barreira, ocorre interferência da onda \(C\), que caminha em direção à segunda interface \((x=a)\), com a onda \(D\), que é refletida por essa interface. Mas, visto que o número de onda dessas ondas é imaginário, as exponenciais complexas se transformam em exponenciais reais.

Quando a interferência é pouco influenciada pela onda refletida, podemos modificar a expressão do coeficiente de transmissão \(T_{\rm b}\), analisando algumas passagens da [ seção 8.2 ].

O que significa, em termos probabilísticos, a onda \(D\) ser pouco influente? Quer dizer que ela carrega pouca probabilidade em relação à onda \(C\). Nesse sentido, podemos considerar que:

\[ |D|^2 \ll |C|^2. \tag{8.37} \]

Na [ seção 8.2 ], deduzimos as expressões das grandezas \(C\) e \(D\). Aqui determinamos:

\[ \begin{aligned} |C|^2 &= \frac{q^2 + k^2}{4q^2} \, |F|^2 \, \mathrm{e}^{\large 2qa} ,\\ |D|^2 &= \frac{q^2 + k^2}{4q^2} \, |F|^2 \, \mathrm{e}^{\large -2qa} . \end{aligned} \tag{8.38} \]

Logo,

\[ \frac{|D|^2}{|C|^2} = \left( \mathrm{e}^{\large -qa} \right) ^4. \tag{8.39} \]

A condição (8.37) é seguramente satisfeita se \(\mathrm{e}^{\large -qa} \ll 1\). O que nos leva a seguinte aproximação:

\[ \mathrm{senh}(qa) = \frac{\mathrm{e}^{\large qa} - \mathrm{e}^{\large -qa}}{2} \cong \frac{\mathrm{e}^{\large qa}}{2}. \tag{8.40} \]

Vamos utilizar (8.40) para encontrar um valor aproximado de \(T_{\rm b}\):

\[ \frac{1}{T_{\rm b}} = 1 + \frac{\left( k^2 + q^2 \right)^2}{4k^2q^2} \, {\rm senh}^2(qa), \tag{8.41} \]

\[ \frac{1}{T_{\rm b}} \cong 1 + \frac{\left( k^2 + q^2 \right)^2}{16k^2q^2} \, \mathrm{e}^{\large 2qa}. \tag{8.42} \]

Como \(\mathrm{e}^{\large 2qa} \gg 1\), o número “\(1\)” que aparece em (8.42) pode ser desprezado, logo:

\[ T_{\rm b} \cong \frac{16k^2q^2}{\left( k^2 + q^2 \right)^2} \, \mathrm{e}^{\large -2qa}. \tag{8.43} \]

Na próxima [ seção 8.6 ], vamos usar (8.43) para entender o funcionamento do Microscópio de Varredura por Tunelamento.

8.6 O STM

STM é a sigla de Scanning Tunneling Microscopy, Microscópio de Varredura por Tunelamento.

O STM se alicerça no fenômeno quântico do tunelamento. Quando a ponta metálica de um STM se aproxima de um material condutor (metal ou semicondutor dopado), entre a ponta e o condutor se forma uma barreira de potencia \(V_0\), de largura \(a\), igual à distância entre a ponta e o condutor. Pelo efeito de tunelamento, elétrons da ponta têm probabilidade de se transferirem para o condutor. A topografia da superfície do condutor pode ser mapeada fazendo a ponta do STM se movimentar sobre o condutor. Há dois modos de operação: o modo de altura constante e o modo de corrente constante. A Fig. 8.3 apresenta os detalhes desses modos de operação.

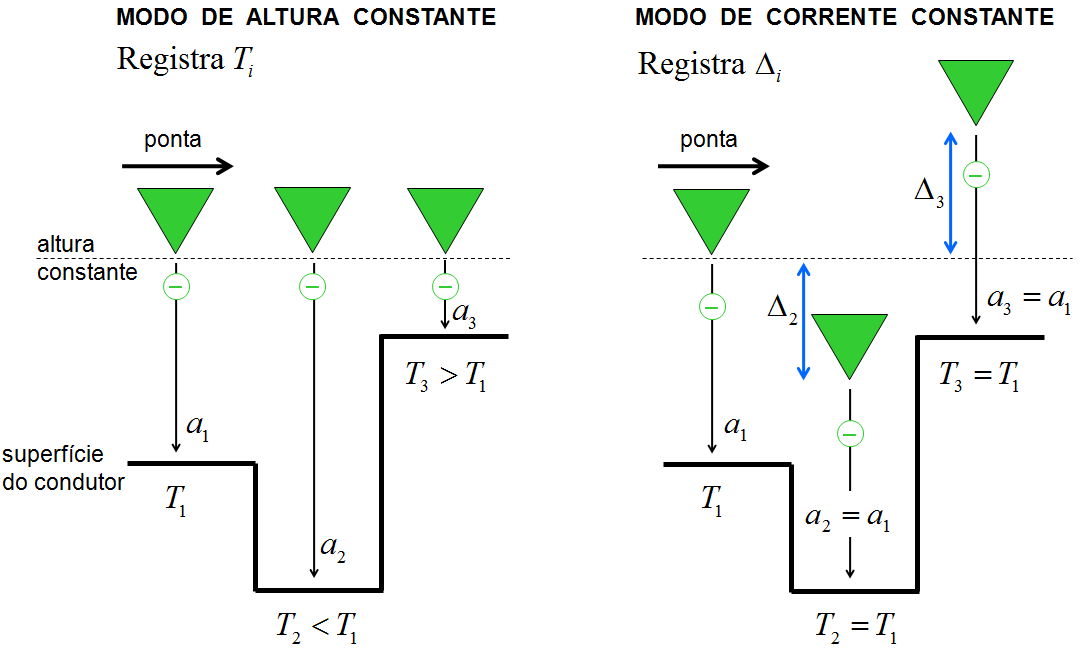
Figura 8.3: Os modos de operação de um STM.

No modo de altura constante, cada ponto sobre o condutor, de posição \(x_i\), forma uma barreira de largura \(a_i\), sendo \(i=1, 2, 3, {\rm etc}\). Para cada \(a_i\), há uma probabilidade de tunelamento \(T_i\). Conforme vimos na [ seção 8.5 ], \(T_i \cong \mathrm{e}^{\large -2qa_i}\). Se há \(N\) elétrons livres na ponta do microscópio, a quantidade \(NT_i\) fará parte da corrente de tunelamento \(I_i\), ou seja, \(I_i \cong NT_i\). Portanto, o STM vai registrar uma corrente de tunelamento diferente para cada ponto investigado. Ao traçar a corrente \(I_i\) em função da posição da ponta sobre o condutor \(x_i\), teremos a imagem da superfície do material.

No modo de corrente constante, o registro é feito no deslocamento vertical da ponta do microscópio, indicado por \(\Delta\) na Fig. 8.3. No primeiro ponto em estudo, ajustamos a corrente base do processo: \(I_1\). Sabemos que a próxima corrente \(I_i\), depende de \(T_i\), que por sua vez, depende de \(a_i\). Ao fazer a varredura, podemos, então, ajustar \(I_i\) para ter o mesmo valor da corrente base \(I_1\). Como fazemos isso? Liberando a ponta do microscópio para se movimentar na vertical. Portanto, o STM vai registrar um deslocamento vertical para cada ponto investigado. Ao desenhar \(\Delta _i\) em função de \(x_i\), veremos a imagem da superfície do material.

8.7 O fluxo de probabilidade pela barreira

Antes de avançar, seria importante recordar a nomenclatura utilizada para caracterizar a barreira retangular [ ver seção 8.2 ]. Como dissemos, a onda de matéria incidente \(A\) pode aparecer do outro lado da barreira, na forma da onda transmitida \(F\), ou aparecer na frente da barreira, na forma da onda refletida \(B\).

A densidade de probabilidade do estado incidente \(A\), a grandeza \(|A|^2\), significa probabilidade por unidade de comprimento. Ela pode ser transformada em probabilidade por unidade de tempo, que chamaremos de fluxo de probabilidade \(j_A\). Para fazer a transformação, precisamos levar em conta a velocidade com que o estado \(A\) avança em direção à barreira:

\[ v = \frac{\hbar k}{m}. \tag{8.44} \]

A transformação ocorre se definirmos:

\[ j_A = v|A|^2. \tag{8.45} \]

Lembrando que velocidade tem dimensão dada por comprimento\(/\)tempo, fica claro que (8.45) tem dimensão de probabilidade\(/\)tempo.

Vamos então listar todos fluxos de probabilidade que ocorrem na barreira retangular:

\[\begin{align} j_A &= v|A|^2, \tag{8.46} \\ j_B &= - v|B|^2, \tag{8.47} \\ j_F &= v|F|^2. \tag{8.48} \end{align}\]

Já falamos do fluxo de probabilidade incidente (8.46), mas também existe o fluxo de probabilidade refletica (8.47) e o fluxo de probabilidade transmitida (8.48). Fica claro que o fluxo total de entrada \(({\rm in})\) e o fluxo total de saída \(({\rm out})\), são:

\[\begin{align} j _ {\rm in} &= j_A + j_B, \tag{8.49} \\ j _ {\rm out} &= j_F. \tag{8.50} \end{align}\]

Nesse novo alicerce teórico, o coeficiente de transmissão é definido como:

\[ T = \frac{j_F}{j_A}. \tag{8.51} \]

Substituindo (8.46) e (8.48) em (8.51), recuperamos o argumento usado na [ seção 8.2 ], quando dissemos que:

\[ T = \frac{|F|^2}{|A|^2}. \tag{8.52} \]

Assim como definimos o coeficiente (8.51), podemos definir o coeficiente de reflexão:

\[ R = \frac{-j_B}{j_A} \ \ \implies \ \ R = \frac{|B|^2}{|A|^2}. \tag{8.53} \]

Nota: Como o valor de (8.47) é negativo, há necessidade da inclusão do sinal \((-)\), para fazer \(R\) ser uma grandeza positiva.

Aqui vale ressaltar que \(T + R = 1\).

Agora, substituindo (8.53) em (8.49), e (8.51) em (8.50), encontramos:

\[\begin{align} j _ {\rm in} &= j_A (1-R) = j_A T, \tag{8.54} \\ j _ {\rm out} &= j_A T. \tag{8.55} \end{align}\]

Portanto, o fluxo total pela barreira é constante: \(j_{\rm out} = j_{\rm in}\).

8.8 A origem do fluxo de probabilidade

Na [ seção 8.7 ], introduzimos a ideia de fluxo de probabilidade. Não nos preocupamos sobre sua origem. Agora vamos desenvolver a fórmulação que dá origem a esse fluxo.

Começamos multiplicando a equação de Schrödinger, equação (8.56), pelo complexo conjugado da função de onda:

\[\begin{align} i\hbar \frac{\partial \Psi}{\partial t} &= -\frac{\hbar ^2}{2m}\frac{\partial ^2 \Psi}{\partial x^2} + V\Psi, \tag{8.56}\\ i\hbar \Psi^{\ast} \frac{\partial \Psi}{\partial t} &= -\frac{\hbar ^2}{2m} \Psi^{\ast} \frac{\partial ^2 \Psi}{\partial x^2} + \Psi^{\ast}V\Psi. \tag{8.57} \end{align}\]

Em seguida, multiplicamos o complexo conjugado da equação de Schrödinger, equação (8.58), pela função de onda:

\[\begin{align} -i\hbar \frac{\partial \Psi^{\ast}}{\partial t} &= -\frac{\hbar ^2}{2m}\frac{\partial ^2 \Psi^{\ast}}{\partial x^2} + V\Psi^{\ast}, \tag{8.58}\\ -i\hbar \Psi \frac{\partial \Psi^{\ast}}{\partial t} &= -\frac{\hbar ^2}{2m} \Psi \frac{\partial ^2 \Psi^{\ast}}{\partial x^2} + \Psi V\Psi^{\ast}. \tag{8.59} \end{align}\]

Por fim, subtraímos os resultados (8.57) e (8.59):

\[ i\hbar \left( \Psi^{\ast} \frac{\partial \Psi}{\partial t} + \Psi \frac{\partial \Psi^{\ast}}{\partial t} \right) = -\frac{\hbar ^2}{2m} \left( \Psi^{\ast} \frac{\partial ^2 \Psi}{\partial x^2} + \Psi \frac{\partial ^2 \Psi^{\ast}}{\partial x^2} \right). \tag{8.60} \]

Usando da matemática, os parênteses de (8.60) são:

\[\begin{align} \Psi^{\ast} \frac{\partial \Psi}{\partial t} + \Psi \frac{\partial \Psi^{\ast}}{\partial t} &= \frac{\partial}{\partial t} \left( \Psi^{\ast} \Psi \right), \tag{8.61} \\ \Psi^{\ast} \frac{\partial ^2 \Psi }{\partial x^2} + \Psi \frac{\partial ^2 \Psi^{\ast}}{\partial x^2} &= \frac{\partial }{\partial x} \left( \Psi^{\ast} \frac{\partial \Psi}{\partial x} - \Psi \frac{\partial \Psi^{\ast}}{\partial x} \right). \tag{8.62} \end{align}\]

Utilizando (8.61) e (8.62) em (8.60), temos:

\[ \frac{\partial}{\partial t} \left( \Psi^{\ast} \Psi \right) = -\frac{\partial}{\partial x} \left[ \frac{\hbar}{2mi} \left( \Psi^{\ast} \frac{\partial \Psi}{\partial x} - \Psi \frac{\partial \Psi^{\ast}}{\partial x} \right) \right] . \tag{8.63} \]

Observa-se que (8.63) relaciona a densidade de probabilidade, \(\rho\), com o fluxo de probabilidade, \(j\), onde:

\[\begin{align} \rho &= \Psi^{\ast} \Psi , \tag{8.64} \\ j &= \frac{\hbar}{2mi} \left( \Psi^{\ast} \frac{\partial \Psi}{\partial x} - \Psi \frac{\partial \Psi^{\ast}}{\partial x} \right). \tag{8.65} \end{align}\]

Logo, (8.63) pode ser escrita na forma compacta:

\[ \frac{\partial \rho}{\partial t} + \frac{\partial j}{\partial x} = 0. \tag{8.66} \]

A densidade de probabilidade e o fluxo de probabilidade estão interligados através da conhecida equação da continuidade, que surge no contexto da mecânica dos fluidos e também na eletrodinâmica clássica. Na mecânica dos fluidos, ela atesta em última análise a conservação da massa, e na eletrodinâmica, a conservação da carga. No presente contexto da mecânica quântica, ela reflete a conservação da probabilidade. Para entender melhor essa ideia, vamos fazer um jogo de palavras com as palavras probabilidade e elétrons:

“Num dado instante, e em num dado local, se o fluxo de entrada de elétrons for maior que o fluxo de saída, \({\partial j}/{\partial x} < 0\), aumenta a concentração de elétrons desse local, \({\partial \rho}/{\partial t} >0\), mas, se o fluxo de entrada for igual ao fluxo de saída, \({\partial j}/{\partial x} = 0\), a concentração de elétrons não se altera, \({\partial \rho}/{\partial t} = 0\).”

Vamos calcular o fluxo de probabilidade do estado incidente \(A\):

\[ \psi_{\rm A} = A\, \mathrm{e}^{\large ikx}\, \mathrm{e}^{\large \frac{-iE}{\hbar} t} \ \ \implies \ \ \psi_{\rm A}^{\ast} = A^{\ast}\, \mathrm{e}^{\large -ikx}\, \mathrm{e}^{\large \frac{iE}{\hbar} t}. \tag{8.67} \]

Utilizando a definição (8.65) em (8.67), encontramos:

\[ \begin{aligned} j_A &= \frac{\hbar}{2mi} \left( ik|A|^2 + ik|A|^2 \right) \\ &= \frac{\hbar k}{m} |A|^2 \\ &= v |A|^2 . \end{aligned} \tag{8.68} \]

O fluxo \(j_A\) não depende da posição, \({\partial j_A}/{\partial x} = 0\). Assim, a aquação de continuidade (8.66) implica em \({\partial \rho_A}/{\partial t} = 0\), quer dizer, a densidade de probabilidade é constante. De fato, \({\rho_A} = |A|^2\).

Nota: A barreira que estamos usando como ilustração é unidimensional. Assim, \(\rho\) é probabilidade por comprimento. Isso leva \(j\) a ser probabilidade por tempo. Porém, se o sistema fosse tridimensional, \(\rho\) seria probabilidade por comprimento\(^3\). O que, por sua vez, levaria \(j\) a ser probabilidade por (tempo \(\cdot\) comprimento\(^2\)).

8.9 A normalização do inormalizável

Nem sei se a palavra \(``\)inormalizável\("\) será ou não incorporada aos dicionários. Mas sei que algumas funções de onda da mecânica quântica trazem em si o conceito de \(``\)aquilo que se não consegue normalizar\("\). É o caso das ondas que caminham fora da barreira retangular [ seção 8.2 ], por exemplo, a onda incidente é representada por:

\[ \psi_{\rm A} = A\, \mathrm{e}^{\large ikx}._{} \tag{8.69} \]

A normalização da função de onda (8.69) resulta em:

\[ \int_{-\infty}^{+\infty} |\psi_A|^2 \mathrm{d}x = |A|^2 \int_{-\infty}^{+\infty} \mathrm{d}x {\small \rm \ \ [resultado\ divergente]}. \tag{8.70} \]

Tais funções são características de estados não-ligados. Se uma função de onda representa um estado ligado, como as funções de onda do poço retangular infinito [ ver seção 6.2 ], então, quando fazemos a normalização, o resultado é finito.

Apesar da integral (8.70) divergir, ela é bem definida quando realizada em uma porção finita do espaço. Por exemplo, podemos fazer a integral considerando apenas certo comprimento \(L = x_2 - x_1\), localizado na frente da barreira:

\[ \int_{x_1}^{x_2} |\psi_A|^2 \mathrm{d}x = |A|^2 \int_{x_1}^{x_2} \mathrm{d}x = |A|^2 L {\small \rm \ \ [total\ de\ partículas]}. \tag{8.71} \]

Se chamarmos, o total de partículas em \(L\) de \(N\), então,

\[ n = \frac{N}{L}, \tag{8.72} \]

será a densidade de partículas incidentes, e, nesse caso:

\[ |A|^2 = n. \tag{8.73} \]

Contornamos o problema da \(``\)inormalização\("\). Agora somos capazes de dar condições de normalização ao problema dos estados não-ligados. Olhando para (8.73), se optarmos que a amplitude da onda incidente seja real, teremos \(|A|^2=A^2\), daí:

\[ A = \sqrt{n}. \tag{8.74} \]

Na [ seção 8.7 ], deduzimos que \(|B|^2 = R|A|^2\) e \(|F|^2 = T|A|^2\), agora, com a dedução (8.73), podemos escrever:

\[\begin{align} |B|^2 = n R, \ \ \implies \ \ n_R = n R, \tag{8.75} \\ |F|^2 = n T, \ \ \implies \ \ n_T = n T. \tag{8.76} \end{align}\]

Portanto, ao definir que \(|A|^2\) é igual a densidade de partículas incidentes, \(|B|^2\) se torna igual à densidade de partículas refletidas, conforme (8.75), e \(|F|^2\) se torna igual à densidade de partículas transmitidas, segundo (8.76)

Ademais, como não há criadouro ou sumidouro de partículas:

\[ n = n_R + n_T. \tag{8.77} \]

Trabalhar com grandezas ligadas à partícula parece mais intuitivo do que ligadas à probabilidade. De fato, para uma barreira exposta a um feixe de partículas incidentes \(n\), podemos usar a intuição e reescrever os fluxos de probabilidade, desenvolvidos na [ seção 8.7 ], em termos de fluxos de partículas:

\[\begin{align} j_A &= v n &{\small \rm [fluxo\ de\ partículas\ incidentes]} \tag{8.78}\\ \notag \\ j_B &= -v n_R &{\small \rm [fluxo\ de\ partículas\ refletidas]} \tag{8.79}\\ \notag \\ j_F &= v n_T &{\small \rm [fluxo\ de\ partículas\ transmitidas]} \tag{8.80}\\ \notag \\ j _ {\rm in} &= v(n - n_R) &{\small \rm [fluxo\ total\ na\ entrada\ da\ barreira]} \tag{8.81}\\ \notag \\ j _ {\rm out} &= v n_T &{\small \rm [fluxo\ total\ na\ saída\ da\ barreira]} \tag{8.82} \end{align}\]

Ademais, também podemos reescrever os coeficientes de transmissão e de reflexão:

\[\begin{align} T &= \frac{n_T}{n} &{\small \rm [coeficiente\ de\ transmissão]} \tag{8.83}\\ \notag \\ R &= \frac{n_R}{n} &{\small \rm [coeficiente\ de\ reflexão]} \tag{8.84} \end{align}\]